
By Lars Brink*
Forces
One of the basic features in physics is the occurrence of forces that keep matter together. There are for example, the forces that keep the cells together to build up the human body, and there is the gravitational force that keeps us on the ground and the moon in orbit around the earth. We can ourselves exert forces when we push something and, by engineering, get some of the energy content in oil to produce a force on the wheels of a car to move it. From the macroscopic point of view we can imagine many different kinds of forces, forces that act at impact but also forces that act over a distance such as the gravitational one. In physics, though, we try to systematise and to find as many general concepts as possible. One such systematisation is to find out the ultimate constituents of matter. Another is to find out the forces that act between them. In the first case, we have been able to divide up matter into atoms and the atoms into nuclei and electrons, and then the nuclei into protons and neutrons. By colliding protons with protons or protons with electrons, particle physicists have uncovered that all matter can be built from a number of quarks (a concept introduced by Murray Gell-Mann in the 60’s) and leptons (electrons and neutrinos and their heavier cousins). In the same process physicists have uncovered four basic forces that act between these matter particles – gravitation, electromagnetism, the strong and the weak nuclear force. Only the first two can be directly seen in the macroscopic world so let us first describe them.

Gravitation
The first quantitative theory of gravitation based on observations was formulated by Isaac Newton in 1687 in his Principia. He wrote that the gravity force that acts on the sun and the planets depends on the quantity of matter that they contain. It propagates to large distances and diminishes always as the inverse of the square of the distance. The formula for the force F between two objects with masses m1 and m2 a distance raway is thus
F=Gm1m2/r2,
where G is a constant of proportionality, the gravitational constant. Newton was not fully happy with his theory since it assumed an interaction over a distance. This difficulty was removed when the concept of the gravity field was introduced, a field that permeates space. Newton’s theory was very successfully applied to celestial mechanics during the 18th and the beginning of the 19th century. For example J.C. Adams and U.J.J. Leverrier were able to conjecture a planet outside of Uranus from irregularities in its orbit and subsequently, Neptune was found. One problem remained though. Leverrier had in 1845 calculated that Mercury’s orbit precesses 35” per century in contrast to the Newtonian value that is zero. Later measurements gave a more precise value of 43”. (The observed precession is really 5270”/century, but a painstaking calculation to subtract the disturbances from all the other planets gives the value of 43”.) It was not until 1915 that Albert Einstein could explain this discrepancy.
Galilei was the first to observe that objects seemingly fall at the same speed regardless of their masses. In Newton’s equations the concept of mass occurs in two different equations. The second law says that a force F on a body with mass m gives an acceleration a according to the equation F=ma. In the law of gravity, the force of gravity F satisfies F=mg, where g depends on the other bodies exerting a force on the body (the earth usually, when we talk of the gravity force). In both equations m is a proportionality factor (the inertial mass and the gravitational mass) and there is no obvious reason that they should be the same for two different objects. However, all experiments indicate that they are. Einstein took this fact as the starting point for his theory of gravitation. If you cannot distinguish the inertial mass from the gravitational one you cannot distinguish gravitation from an acceleration. An experiment performed in a gravity field could instead be performed in an accelerating elevator with no gravity field. When an astronaut in a rocket accelerates to get away from earth he feels a gravity force that is several times that on earth. Most of it comes from the acceleration. If one cannot distinguish gravity from acceleration one can always substitute the gravity force by being in an accelerating frame. A frame in which the acceleration cancels the gravity force is called an inertial frame. Hence the moon orbiting the earth can instead be regarded to be in an accelerating frame. However this frame will be different from point to point since the gravity field changes. (In the example with the moon the gravity field changes direction from one point to another.) The principle that one can always find an inertial frame at every point of space and time in which physics follows the laws in the absence of gravitation is called the Equivalence Principle.
 |
The fact that the gravitational force can be thought of as coordinate systems that differ from point to point means that gravity is a geometric theory. The true coordinate system that covers the whole of space and time is hence a more complex one than the ordinary flat ones we are used to from ordinary geometry. This type of geometry is called Non Euclidean Geometry. The force as we see it comes from properties of space and time. We say that space-time is curved. Consider a ball lying on a flat surface. It will not move, or if there is no friction, it could be in a uniform movement when no force is acting on it. If the surface is curved, the ball will accelerate and move down to the lowest point choosing the shortest path. Similarly, Einstein taught us that the four-dimensional space and time is curved and a body moving in this curved space moves along a geodesics which is the shortest path. Einstein showed that the gravity field is the geometric quantity that defines the so-called proper time, which is a concept that takes the same value in all coordinate systems similar to distance in ordinary space. He also managed to construct equations for the gravity field, the celebrated Einstein’s equations, and with these equations he could compute the correct value for the precession for the orbit of Mercury. The equations also give the measured value of the deflection of light rays that pass the sun and there is no doubt that the equations give the correct results for macroscopic gravitation. Einstein’s theory of gravitation, or General Relativity, as he called it himself is one of the greatest triumphs of modern science.

Electromagnetism
It was James Clark Maxwell who, in 1865, finally unified the concepts of electricity and magnetism into one theory of electromagnetism. The force is mediated by the electromagnetic field. The various derivatives of this field lead to the electric and the magnetic fields, respectively. The theory is not totally symmetric in the electric and the magnetic fields though, since it only introduces direct sources to the electric field, the electric charges. A fully symmetric theory would also introduce magnetic charges, (predicted to exist by modern quantum theory but with such huge magnitudes that free magnetic charges must be extremely rare in our universe). For two static bodies with charges e1 and e2 the theory leads to Coulomb’s Law giving the force
F=ke1e2/r2,
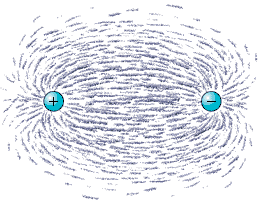
where again k is a proportionality constant. Note the resemblance with Newton’s law for gravity. There is one difference though. While the gravitational force always is attractive, the electromagnetic one can also be repulsive. The charges can either have negative signs such as for the electron or be positive as for the proton. This leads to the fact that positive and negative charges tend to bind together such as in the atoms and hence, screen each other and reduce the electromagnetic field. Most of the particles in the earth screen each other in this way and the total electromagnetic field is very much reduced. Even so we know of the magnetic field of the earth. Also in our bodies most charges are screened so there is a very minute electromagnetic force between a human being and the earth. The situation is very different for the gravity field. Since it is always attractive, every particle in the earth interacts with every particle in a human body, setting up a force with is just our weight. However, if we compare the electromagnetic and the gravitational forces between two electrons we will find that the electromagnetic one is bigger by a factor which is roughly 1040. This is an unbelievably large number! It shows that when we come to microcosm and study the physics of elementary particles we do not need to consider gravity when we study quantum electrodynamics, at least not at ordinary energies.
 |
When examining Maxwell’s equations one finds that the electromagnetic field travels with a finite velocity. This means that Coulomb’s Law is only true once the electromagnetic field has had time to travel between the two charges. It is a static law. One also finds that the electromagnetic field travels as a wave just in the same way as light does. It was Rømer who discovered that the velocity of light is finite and Newton and Huygens who discovered that light travels as waves in the late 17th century, and by the end of the 19th century the velocity of light was well established and seen to agree with the velocity of the electromagnetic field. Hence it was established that light is nothing but electromagnetic radiation. In 1900 Max Planck proposed that light is quantised in order to explain the black body radiation. However, it was Albert Einstein who was the first to really understand the revolutionary consequences of this idea when he formulated the photoelectric effect. The electromagnetic field can be understood as a stream of corpuscular bodies to be called photons that make up the electromagnetic field. The revolutionary aspect of this idea was that a stream of particles also could behave as a wave and there was much opposition to the idea from many established scientists of the day. It was not until 1923 when Arthur Compton experimentally showed that a light quanta could deflect an electron just like a corpuscular body would do it, that this debate was over.
If we think about the electric force between two charges as the electromagnetic field mediating it over a distance, we can now get a more fundamental picture as a stream of photons sent out from one particle to hit the other. This is a more intuitive picture than a force acting over a distance. Our macroscopic picture of a force is that something hits a body that then feels a force. In the microscopic world this is then again a way to understand a force. However, it is more complex. Suppose there are two charged particles that interact. Which particle is sending out a photon and which is receiving the photon if the two particles are identical as quantum mechanics tells us about fundamental particles? The answer must be that the picture should include both possibilities. The discovery that the electromagnetic field is quantised started the development of quantum mechanics and led us to a microcosm that is just built up by point-like objects and where forces occur when two particles hit each other.
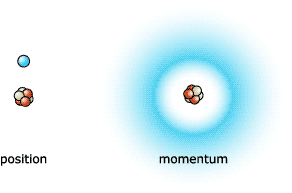
Quantum mechanics as such led to many new revolutionary concepts. One of the most important ones is Heisenberg’s Uncertainty Relation formulated by Werner Heisenberg in 1927, which states that one cannot measure position and momentum or energy and time exactly simultaneously. For a nucleus, one can either determine the position of an electron and know nothing of its momentum or know its momentum and nothing about its position. In the picture showing the force field between two charges, we should think of it as photons travelling from one charge to another. Hence the energy cannot be determined better than what the uncertainty relation tells us because of the uncertainty in the determination of the time. Hence the special relativity relation for light that the photon is massless which translates into the relation that the energy2=momentum2c2 need not be satisfied. If we put the energy and the tree-dimensional momentum together into the four-momentum we see that it is not constrained by the masslessness condition, we say that the photon is virtual and consequently has a (virtual) mass. We can thus interpret the process above as either a certain photon going from particle 1 to particle 2 with a certain four-momentum or as one from particle 2 to particle 1 with the opposite four-momentum. When two charges are far away the uncertainty relation gives little freedom and the photon is closer to masslessness, We know that Coulomb’s law seems to be valid at the longest distances so it must be set up by the photons close to masslessness. If two charges are close there should be more terms to the force. Incidentally in order to measure the velocity of light the photons must interact. Hence there is a slight uncertainty in its mass and a slight uncertainty in its velocity. However, we measure always the same velocity for light which means that at the macroscopic distances that we measure, the virtuality and hence the mass of the photon is essentially zero to a very good accuracy. It is then consistent to say that the velocity of light is constant.
The full description of the electromagnetic force between elementary particles was formulated by Sin-Itiro Tomonaga, Richard Feynman and Julian Schwinger in independent works in the 1940’s. They formulated Quantum ElectroDynamics (QED). This is a theory that takes full account of quantum physics and special relativity (which is the underlying symmetry of Maxwell’s Equations). It is very elegantly formulated by so-called Feynman diagrams, where the elementary particles exchange photons as was described above and where each diagram constitutes a certain mathematical expression that can be obtained from some basic rules for the propagation of virtual particles and from the interaction vertices. The simplest diagram for the interaction between two electrons is
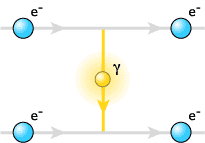 |
This diagram in fact leads to Coulomb’s law. Feynman now instructs us that we can combine any line for a propagating electron (or when it travels backwards, the positron) and any line for a propagating photon tied together with the vertex where an electron line emits a photon to make up new diagrams. Every other diagram differing from the one above constitutes quantum corrections to the basic force. It was through the work of the three scientists above that it was shown that every such diagram can be made to make sense to give finite answers. It is said that QED is renormalisable. The strength of the force as in Coulomb’s law is governed by the magnitude of the vertex which is the electric charge e in QED and for the diagram above it is proportional to the square of e and is the Fine Structure Constant ![]() = 1/137. Since this is a small number it makes sense to write the amplitude in a series of terms with higher and higher powers of
= 1/137. Since this is a small number it makes sense to write the amplitude in a series of terms with higher and higher powers of ![]() since that factor will be smaller and smaller for ever increasing complexity of the diagram. The higher order terms are higher quantum corrections and the perturbation expansion that we have defined will have smaller and smaller terms as we go to higher quantum corrections.
since that factor will be smaller and smaller for ever increasing complexity of the diagram. The higher order terms are higher quantum corrections and the perturbation expansion that we have defined will have smaller and smaller terms as we go to higher quantum corrections.
Nuclear forces
Since there were only two basic forces known in the beginning of the 20th century, gravitation and electromagnetism, and it was seen that electromagnetism is responsible for the forces in the atom, it was natural to believe that it was also responsible for the forces keeping the nucleus together. In the 1920’s it was known that the nuclei contain protons, in fact the hydrogen nucleus is just a proton, and somehow it was believed that electrons could be involved in keeping the protons together. However, an idea like this has immediate problems. What is the difference between the electrons in the nucleus and the ones in orbit around the nucleus? What is the consequence of Heisenberg’s uncertainty relation if electrons are squeezed into the small nucleus? The only support for the idea, apart from there being no other known elementary particles, was that in certain radioactive decays electrons were seen to come from the nucleus. However, in 1932 James Chadwick discovered a new type of radiation that could emanate from the nuclei, a neutral one and his experiment showed that there are indeed electrically neutral particles inside the nuclei, which came to be called neutrons. Soon after Eugene Wigner explained the nuclei as a consequence of two different nuclear forces. The Strong Nuclear Force is an attractive force between protons and neutrons that keep the nucleus together and the Weak Nuclear Force is responsible for the radioactive decay of certain nuclei. It was realized that the strength of the two forces differed a lot. The typical ratio is of the order of 1014 at ordinary energies.
Strong interactions
A natural idea now was to search for a mechanism like the one in electromagnetism to mediate the strong force. Already in 1935 Hideki Yukawa proposed a field theory for the strong interaction where the mediating field particle was to be called a meson.
However, there is a significant difference between the strong force and the electromagnetic one in that the strong force has a very short range (typically the nuclear radius). This is the reason why it has no classical counterpart and hence had not been discovered in classical physics. Yukawa solved this problem by letting the meson have a mass. Such a particle was also subsequently seemingly found from cosmic rays by Carl Anderson. The discovery of nuclear fission in the late 1930’s led to an enormous interest in nuclear physics and in the war years most physicists worked on problems with fission so it was not until after the war that Yukawa’s ideas were taken up again. It was then realized that the particle found by Anderson could not be the meson of strong interactions, since it interacted far too little with matter, and it was then shown that this particle, now called the muon, is a heavy cousin of the electron. However, the meson, now called pion, was finally discovered in cosmic rays by Cecil Powell in 1947 and its properties were measured. A new dilemma now appeared. When the big accelerators started to operate in the 1950’s, the pions were produced vindicating Yukawa’s theory, but when his field theory was scrutinised according to the rules set up by Feynman, it was shown that indeed the theory is renormalisable but the coupling constant is huge, larger than one. This means that a diagram with several interactions will give a larger contribution than the naive one with the exchange of only one pion, which is the one though that does gives a rough picture of the scattering of two protons. The perturbation expansion does not make sense. Also the scattering of protons produced new strongly interacting particles beside the pion, which were named hadrons. Indeed a huge menagerie of elementary particles were discovered, some of them with a life time of some 10-8 to 10-10 s and some with a lifetime of 10-23 s. This problem was solved by Murray Gell-Mann when he proposed that all the strongly interacting particles are indeed bound states of even more fundamental states, the quarks. This idea was eventually experimentally verified in the Stanford experiments in the years around 1970 led by Jerome Friedman, Henry Kendall and Richard Taylor. To understand the forces inside the nucleus one really had to understand the field theory for quarks. Before describing the forces between quarks we have to discuss the other nuclear force, the weak one.
Weak interactions
In 1896 Henri Becquerel discovered that uranium salts emit a radiation; they are radioactive. His work was followed up by Marie and Pierre Curie who discovered that several atoms disintegrated by sending out radioactivity. With the discovery of the neutron it was realized that this phenomenon is another aspect of a force at work. It was found that the neutron decays into a proton and an electron and a then hypothetical particle proposed by Wolfgang Pauli, which came to be called the neutrino (really the antineutrino). Since in the nucleus the mass of the nucleons are virtual the process can also go the other way in which a proton decays into a neutron, a positron and a neutrino. The first to set up a model for this interaction was Enrico Fermi in which it was supposed that the interaction was instantaneous among the matter particles. In the late 1950s Fermi’s theory was modified to account for parity violation by Marshak and Sudarshan and by Feynman and Gell-Mann. Parity violation of the weak interactions had been postulated by Tsung-Dao Lee and Chen Ning Yang in 1956 and experimentally verified by Wu and collaborators the year after. (The weak interactions can distinguish between left and right.)
However, the model introduced had severe problems. It is not renormalisable so it cannot really make sense as a general theory. On the other hand the model worked extremely well for many processes. How could one reconcile these two facts? During the 1960’s new field theoretic descriptions were proposed and to reconcile the facts above one introduced mediating particles that were extremely heavy. For low energy processes such a particle can only propagate a very short distance and in practice it will look as if the interaction takes place in one point giving the model above for the energies that at the time could be probed. The scheme used, the so-called ‘Non-Abelian Gauge Theories’ were used by Sheldon Glashow, Steven Weinberg and Abdus Salam in independent works to suggest a model that would generalise the model above. Such a field theory is a generalisation of QED in which there are several mediating particles which also can have self interactions. In the beginning of the 1970’s this scheme of models were proven to be renormalisable and hence good quantum theories by Gerhard ‘tHooft and Tini Veltman. Overwhelming experimental evidence for the model was gathered in the 1970’s and finally in 1983 the mediating particles were discovered at CERN in an experiment led by Carlo Rubbia and Simon van der Meer. Indeed the mediating particles are very heavy, almost 100 times the mass of the proton.
Theory for strong interactions
A remarkable feature of the SLAC experiments that verified the existence of quarks was ‘scaling’. The cross sections for the deep inelastic scattering of electrons on protons depended on fewer kinematical variables for higher energies. The cross sections scaled. This phenomenon was theoretically suggested by James Bjorken and the data showed it clearly. Richard Feynman explained it by assuming that the protons consisted of point-like constituents. To explain scaling these constituents must have a coupling strength that decreases with energy, opposite to the case of QED. This was called ‘asymptotic freedom’. It was quite difficult to believe that a quantum field theory could be asymptotically free since the energy dependence of the coupling constant is due to the screening from pairs of virtual particles. Relativistic quantum mechanics allow for such pairs if they do not live too long. This is due to Heisenberg’s uncertainty principle and the fact that energy is the same as mass according to Einstein’s famous formula.
Asymptotic freedom must mean that the quark charges are antiscreened, which as said was hard to believe to exist in a quantum field theory. However, in 1973, David Gross, David Politzer and Frank Wilczek simultaneously found that for a non-abelian gauge field theory the requirement of asymptotic freedom is satisfied if there are not too many quarks. The key to the solution was that the vector particles mediating the force, the gluons, do indeed antiscreen. This can be understood since the charges of the quarks and the gluons, the “colour charges” satisfy more complicated relations than the simpler electric charges. There are three different colours and their anticolours. While the quarks have a colour charge, the gluons have a colour and an anticolour charge. Hence virtual gluons can line up with charges screening each other while the strength of the field increases.
The discovery of asymptotic freedom opened up for a non-abelian gauge field theory for the interactions among quarks and it was called QuantumChromodynamics, QCD. Over the years this theory has been very successfully tested at the large accelerators and it is now solidly established as the theory of the strong interactions.
The standard model
The success of non-abelian gauge theories showed that all the interactions could be unified in a common framework. This led to the so-called Standard Model in which all the matter particles are treated together, i.e. the electron and its heavier partners the muon and the tau-particle and the corresponding neutrinos, which all have only weak interactions, together with the quarks which can have both strong and weak interactions. The force particles, i.e. the mediators, are then the photon for electromagnetism, the W and Z particles for the weak force and the gluons for the strong force. Even though the Standard Model unifies the interactions there are differences in the details. The photon and the gluons are massless particles while the W and Z particles have a mass. The photon leads to Coulomb’s law for large distances while the gluons lead to a confining force between the quarks. This is in fact due to the asymptotic freedom, which can also be interpreted to say that the coupling strength increases with lower energy, which quantum mechanically also means that it increases with distance. In fact this increase is like the one for a spring, such that the quarks are permanently bound in the hadrons. Even so the properties of the gluons have been firmly established by experimenters.
 |
Unification of all interactions
In the standard model above there is no mentioning of the gravitational force. It has been said that it is so tremendously weak that we do not need to take it into account at particle experiments. However, on general grounds there must be a quantum version of the gravity force that acts at small enough distances. If we try to just copy the quantisation of the electromagnetic field in terms of photons we should quantize the gravity field into so-called gravitons. However, the procedure of Feynman, Tomonaga and Schwinger does not work here. Einstein’s gravity is non-renormalisable. Where is the problem? Is it Einstein’s theory or quantum mechanics that is not complete? The two great conceptual milestones of the 20th century, Quantum Mechanics and Einstein’s General Relativity are simply not consistent with each other. Einstein thought for his whole life that quantum mechanics is indeed incomplete, but so many tests of it have by now been made that physicists are instead trying to generalise Einstein’s theory. The remarkable success with the Standard Model has also shown that the idea of unification of the forces is a valid one. Why are there four different forces or are they really different? They do indeed, show up as different forces in the experiments we do, but the Standard Model shows that the electromagnetic and the weak forces are unified for energies above 100 GeV. Similarly the model shows that also the strong force seemingly so different unifies with the other one at energies above 1015GeV. Can the gravitational one be fit into this scheme?
It can be shown that at energies of the order of 1019 GeV the gravity force will be as strong as the other ones, so there should be a unification of all the forces at least at that energy, which is an energy so unbelievably high that it has only occurred in our universe at a time 10-42 s after the Big Bang. However, physics should also be able to describe phenomena that occurred then, so there should be a unified picture which also includes gravity. Such a scheme has now been proposed, The Superstring Model in which particles are described by one-dimensional objects, strings. This model indeed gives Einstein’s theory for low energies and can be made compatible with the Standard Model at the energies where it has been probed. It is also a finite quantum theory so a perturbation theory for gravity based on the Superstring Model is indeed consistent. It is still too early to say if this is the final ‘theory of everything’, but there is no paradox or inconsistency in the model as far as has been understood. Finally the model makes one more unification, namely of the matter particles and the force particles, having just one sort of particles. This is also the ultimate goal of physicists, to have one unified force and one unified kind of particles.
* Lars Brink was born in 1943. He has been a professor of theoretical elementary particle physics since 1986 at Chalmers University of Technology in Göteborg, Sweden. He was a fellow in the Theory Group at CERN, 1971-73 and was an scientific associate at Caltech, 1976-77. He has been a visiting scientist for longer and shorter periods at CERN, Caltech, ITP in Santa Barbara as well as many other institutions around the world at numerous occasions. He was vice dean of physics at Chalmers, 1987-93 and was the chairman of the board of Nordita in Copenhagen, 1990-93 and a member of the board in 1993-97. He is the chairman of the board of International Center for Fundamental Physics in Moscow since 1993. He was elected as member of the Swedish Royal Academy of Sciences in 1997 and as member of its Nobel Committee for Physics in 2001. He is also the coordinator of the EU Network “Superstring Theory” since the year 2000. His scientific work has been mainly in elementary particle theory especially in the attempts to unify all fundamental interactions. He is one of the pioneers of the Superstring Theory and has also been much involved in supersymmetric quantum field theories. One highlight here is the construction and proof of the first finite quantum field theory in four spacetime dimensions.
First published 9 August 2001