Popular information
English
Swedish
The 2003 Nobel Prize in Physics
The quantum physics that controls the micro-world has a wide range of spectacular effects that do not normally occur in our ordinary macro-world. There are, however, certain situations in which quantum phenomena are visible. This year’s Nobel Prize in Physics is awarded for work concerning two of these situations: superconductivity and superfluidity. Alexei Abrikosov and Vitaly Ginzburg have developed theories for superconductivity and Anthony Leggett has explained one type of superfluidity. Both superconductivity and superfluidity occur at very low temperatures.
Flow without resistance
An unexpected cold effect
When investigations were first carried out into the nature of electricity in the 19th century, it was evident that metals and certain alloys conduct electricity by allowing electrons to move between the atoms. But the disorganised way in which the electrons move causes the atoms to vibrate, so heat is generated. If the current is too strong, the heat can be so great that the conductor melts. In addition it was found that an electric current through a conductor creates a magnetic field, which in turn generates current in the opposite direction. Electricity and magnetism interact and can thus counteract each other.
In 1911 the Dutch physicist Heike Kamerlingh Onnes made a remarkable discovery. He was particularly interested in the properties of substances at low temperatures and had succeeded in producing liquid helium, which has an extremely low temperature. When Onnes investigated the electric conductivity of mercury, he found that when the metal was cooled by means of liquid helium to a few degrees above absolute zero, its electric resistance vanished. He named this phenomenon superconductivity. Although no theoretical explanation could be found for this phenomenon, it was evident that it could have far-reaching significance in a modern society that was becoming more and more dependent on electricity. Onnes was awarded the Nobel Prize in Physics in 1913 for this work.
Superconductors of two types
Almost 50 years passed before the physicists John Bardeen, Leon Cooper and Robert Schrieffer (Nobel Prize in Physics, 1972) were able to present a theory (the BCS theory, named after the initials of their surnames) that explained the phenomenon. This theory shows that some of the negatively-charged electrons in a superconductor form pairs, called Cooper pairs. These pairs of electrons flow along attracting channels formed by the regular structure of the positively-charged metal atoms in the material. As a result of this combination and interaction the current can flow evenly and superconductivity occurs. The paired electrons are usually thought of as a condensate, similar to the drops of liquid that form in a cooled gas. Unlike an ordinary liquid this “electronic liquid” is superconductive.
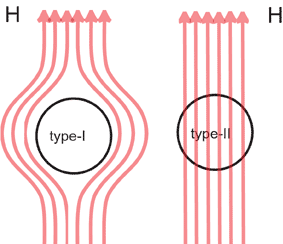
These superconductors are called type-I. They are metals and are characterised by the Meissner effect, that is, in the superconductive state they actively counteract a surrounding magnetic field as long as its strength does not exceed a certain limit (fig. 1). If the surrounding magnetic field becomes too strong, the superconductive property disappears.
High resolution image (jpeg 155 kB)
Fig. 1. Type-I superconductors repel a magnetic field (the Meissner effect). If the strength of the magnetic field increases, they lose their superconductivity. This does not happen with type-II superconductors, which accommodate strong magnetic fields by letting the magnetic field in.
But it is known that there are superconductors that lack or show only a partial Meissner effect. These are in general alloys of various metals or compounds consisting of non-metals and copper. These retain their superconductive property even in a strong magnetic field. Experiments show that the properties of these so-called type-II superconductors cannot be described by the BCS theory.
Alexei Abrikosov, working at the Kapitsa Institute for Physical Problems in Moscow, succeeded in formulating a new theory to describe the phenomenon. His starting point was a description of superconductivity in which the density of the superconductive condensate is taken into account with the aid of an order parameter (a wave function). Abrikosov was able to show mathematically how the order parameter can describe vortices and how the external magnetic field can penetrate the material along the channels in these vortices (fig. 2).
 |
| Fig. 2. This image is of an Abrikosov lattice of vortices in the electron fluid in a type-II superconductor. The magnetic field passes through these vortices. |
Abrikosov was also able to predict in detail how the number of vortices can grow as the magnetic field increases in strength and how the superconductive property in the material is lost if the cores of the vortices overlap. This description was a breakthrough in the study of new superconducting materials and is still used in the development and analysis of new superconductors and magnets. His papers from the late 1950s have been quoted more and more frequently during the past ten years.
The theory Abrikosov’s argument was based on was formulated in the early 1950s by Vitaly Ginzburg and Lev Landau (the latter was awarded the Nobel Prize in Physics in 1962 for other work, see below). This theory was intended to describe superconductivity and critical magnetic field strengths in the superconductors that were known at that time. Ginzburg and Landau realised that an order parameter (wave function) describing the density of the superconductive condensate in the material had to be introduced if the interaction between the superconductor and magnetism was to be explained. When this parameter was introduced, it was evident that there was a breakpoint when a characteristic value approximately 0.71 was reached and that in principle there were two types of superconductor. For mercury the value is approximately 0.16 and other superconductors known at the time have values close to this. There was therefore, at that time, no reason to consider values above the breakpoint. Abrikosov was able to tie up the theory by showing that type-II superconductors had precisely these values.
Our knowledge of superconductivity has led to revolutionary applications (fig. 3). New compounds with superconductive properties are being discovered all the time. In the past few decades a large number of high-temperature superconductors have been developed. The first one was produced by Georg Bednorz and Alex Müller, who were awarded the Nobel Prize in Physics in 1987. All high-temperature superconductors are type-II. Cooling is a critical factor for the utilisation of superconductors. An important limit is 77 K (-196°C), the boiling point of liquid nitrogen, which is cheaper and more manageable than liquid helium.

Fig. 3. An MRI image of a human brain. The resolution in the magnetic resonance camera is dependent partly on the strength of the magnetic field. Today strong superconducting magnets are used, all of them type-II.
Two fascinating superfluids
The lightest rare gas, helium, exists in nature in two forms, two isotopes. The usual form is represented as 4He, where the figure 4 stands for the number of nucleons in the atomic nucleus (two protons and two neutrons). In the unusual form, 3He, the atomic nucleus has only one neutron, so it is lighter. In helium that occurs naturally the heavier isotope is more frequent than the lighter one by a factor of about 10 million. That is why it is only in the last 50 years that it has been possible to produce large amounts of 3He, at nuclear power stations, for example. At normal temperatures the gases of the two isotopes differ only in their atomic weights.
If helium gas is cooled to low temperatures, approximately 4 degrees above absolute zero (-273.15°C), the gas passes into liquid form, it condenses. This happens in the same way as when steam condenses into water. Provided the temperature is not too low, the liquids of the two isotopes have similar properties. Liquid helium is used widely as a coolant, in superconducting magnets, for example. In this case naturally-occurring helium is used, of course, that is, the usual and cheaper form of helium, 4He.
If liquid helium is cooled to even lower temperatures, dramatic differences arise between the liquids of the two isotopes; quantum physical effects appear that cause the liquids to lose all their resistance to internal movement, they become superfluid. This occurs at quite different temperatures for the two superfluids and they exhibit a wide range of fascinating properties, such as flowing freely from openings in the vessel they are kept in. These effects can be explained only by means of quantum physics.
Historic discoveries
The fact that 4He becomes superfluid was discovered by Pyotr Kapitsa, among others, already in the late 1930s. This phenomenon was explained almost immediately by the young theoretician Lev Landau, who was awarded the Nobel Prize in Physics in 1962 for this discovery. (Kapitsa was also awarded the Nobel Prize in Physics, but not until 1978.) The transformation from normal to superconducting liquid, which for 4He occurs at approximately 2 degrees above absolute zero, is an example of Bose-Einstein condensation, a process that has also been observed more recently in gases (cf. the Nobel Prize in Physics awarded in 2001 to Eric Cornell, Wolfgang Ketterle and Carl Wieman).
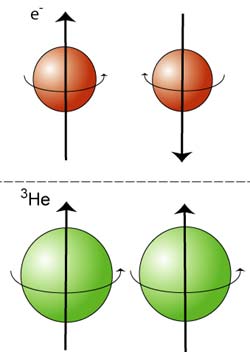
For the 3He isotope the transformation into the superfluid state was not discovered until the early 1970s by David Lee, Douglas Osheroff and Robert Richardson (Nobel Laureates in Physics in 1996). One reason why this discovery came so much later is that the transformation occurs at a very much lower temperature, approximately 1,000 times lower than for 4He. Even though 3He differs in quantum physical respects from 4He and cannot directly undergo Bose-Einstein condensation, this discovery was not unexpected. Thanks to the microscopic theory of superconductivity presented in the 1950s (see above) by Bardeen, Cooper and Schrieffer, there was a mechanism, the formation of Cooper pairs, that ought to have been paralleled in 3He (fig. 4).
 |
| High resolution image (jpeg 315 kB) |
| Fig. 4. The pair formation that occurs in superfluid 3He differs from that which occurs between electrons in a superconductor (Cooper pairs). The magnetic properties of the helium atoms act together, whereas those of the electrons counteract each other. |
The multifarious superfluid
The theoretician who first succeeded in explaining the properties of the new superfluid in a decisive way was Anthony Leggett, who in the 1970s was working at the University of Sussex in England. His theory helped experimentalists to interpret their results and provided a framework for a systematic explanation. Leggett’s theory, which was first formulated for superfluidity in 3He, has also proved useful in other fields of physics, e.g. particle physics and cosmology.
As superfluid, 3He consists of pairs of atoms, its properties are much more complicated than those of the 4He superfluid. In particular the pairs of atoms of the superfluid have magnetic properties, which means that the liquid is anisotropic, it has different properties in different directions. This fact was used in experiments in which studies were made of the liquid immediately after its discovery. By means of magnetic measurements it was revealed that the superfluid has very complex properties, exhibiting a mixture of three different phases. These three phases have different properties and the proportions in the mixture are dependent on temperature, pressure and external magnetic fields (fig. 5).

High resolution image (jpeg 142 kB)
Fig. 5. Superfluid 3He can exist in three phases called A, A1, and B. The type of phase is determined by pressure, temperature and magnetic field according to the figure’s phase diagram.
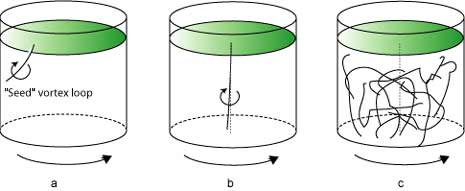
Superfluid 3He is a tool that researchers can use in the laboratory to study other phenomena as well. In particular the formation of turbulence in the superfluid has recently been used to study how order can turn into chaos (fig. 6). This research may lead to a better understanding of the ways in which turbulence arises – one of the last unsolved problems of classical physics.
 |
| High resolution image (jpeg 157 kB) |
| Fig. 6. It has recently been shown that if a vortex is created in a rotating vessel containing superfluid 3He (a), the result can critically depend on the temperature. Above a critical temperature the vortex lines up along the axis of rotation (b). Below the critical temperature a confusion of vortices occurs (c). |
| The Laureates | |
| Alexei A. Abrikosov | |
| Materials Science Division Argonne National Laboratory Bldg. 223 Room B-229 9700 South Cass Ave. Argonne, IL 60439 USA |
American (and Russian) citizen. Born 1928 (75 years) in Moscow, the former Soviet Union. Doctor’s degree in physics in 1951 at the Institute for Physical Problems, Moscow. Distinguished Argonne Scientist, Argonne National Laboratory, Argonne, Illinois, USA. |
| Vitaly L. Ginzburg | |
| P.N. Lebedev Physical Institute Leninskii Pr. 53 117924 Moscow Russia |
Russian citizen. Born 1916 (87 years) in Moscow, Russia. Doctor’s degree in physics at the University of Moscow. Former head of the Theory Group at the P.N. Lebedev Physical Institute, Moscow, Russia. |
| Anthony J. Leggett | |
| Department of Physics University of Illinois at Urbana-Champaign 1110 West Green Street Urbana, IL 61801-3080 USA |
British and American citizen. Born 1938 (65 years) in London, England. Doctor’s degree in physics in 1964 at the University of Oxford. MacArthur Professor at the University of Illinois at Urbana-Champaign, USA. |
Nobel Prizes and laureates
Six prizes were awarded for achievements that have conferred the greatest benefit to humankind. The 14 laureates' work and discoveries range from quantum tunnelling to promoting democratic rights.
See them all presented here.

