Illustrated presentation
The Nobel Prize in Physics 1999
The Royal Swedish Academy of Sciences has awarded the 1999 Nobel Prize in Physics jointly to Professor Gerardus ‘t Hooft and Professor Emeritus Martinus J.G. Veltman for “elucidating the quantum structure of electroweak interactions in physics.”

A theory to reckon with
The structure of particle physics is described using the Standard Model. In this model electromagnetic and weak interactions are unified and together called electroweak interactions. It is theoretical studies of these interactions that have been rewarded with the 1999 Nobel Prize in Physics.

Oven in the sun
The electroweak interactions play an extremely important role in nature. There would be no atoms without electromagnetism and the sun would not shine without weak interactions! Electromagnetic interactions make the electrons keep to their orbits around the nucleus and weak interactions transform protons into neutrons and “bake” them into helium nuclei in the “oven” in the middle of the sun.
‘t Hooft and Veltman did their Nobel Prize work around 1970. Not until results were presented from the particle accelerator LEP at CERN, the European Laboratory in Geneva, was the breadth of their contributions realised. From these results, among other things, the mass of the top quark could be predicted. This prediction was confirmed when the top quark was discovered in 1995 at the Fermi Laboratory outside Chicago.

Further reading
Information on the 1999 Nobel Prize in Physics (press release): The Royal Swedish Academy of Sciences.
Learn more about Particle Physics: www.cern.ch and www.fnal.gov
In search of the Ultimate Building Blocks, by Gerard ‘t Hooft, Cambridge University Press 1997.
The Higgs Boson, by Martinus J.G. Veltman, Scientific American, November 1986, p.88.
Gauge Theories of the Forces between Elementary Particles, by Gerard ‘t Hooft, Scientific American, June 1980, p. 90.
Credits and references for the 1999 Physics Nobel Poster
Editorial Board: Prof. Cecilia Jarlskog, Chair of the Nobel Committee for Physics, and M. Sc. Linda Jarlskog, Lund University, Prof. Anders Bárány, Secretary of the Nobel Committee for Physics, Science Editor Eva Krutmeijer and Dr. Solgerd Björn-Rasmussen, The Royal Swedish Academy of Sciences.
Layout and illustrations: Typoform
Printing: Tryckindustri 1999.
Copyright © The Royal Swedish Academy of Sciences, Information Department, Box 50005, SE-104 05 Stockholm, Sweden, Tel. +46-8-6739500, Fax +46-8-155670, Email: [email protected]
Web adapted version: Nobelprize.org
Every effort has been made by the publisher to credit organizations and individuals with regard to the supply of photographs and illustrations. The publishers apologize for any omissions which will be corrected in future editions.
Pressmeddelande: Nobelpriset i fysik 1999
English
German
French
Swedish

12 October 1999
Kungliga Vetenskapsakademien har utdelat 1999 års Nobelpris i fysik gemensamt till
Professor Gerardus ‘t Hooft, Utrecht Universitet, Utrecht, Nederländerna, och
Professor emeritus Martinus J.G. Veltman, University of Michigan, USA, bosatt i Bilthoven, Nederländerna.
De två forskarna Nobelprisbelönas för att ha satt partikelfysikens teori på fastare matematisk grund. De har speciellt visat hur teorin kan användas för precisa beräkningar av fysikaliska storheter. Experiment vid acceleratorlaboratorier i Europa och USA har nyligen bekräftat många av de beräknade resultaten.
Vetenskapsakademiens motivering:
“för deras avgörande insatser rörande kvantstrukturen hos teorin för elektrosvag växelverkan i fysiken.”
Partikelfysikens teori på fastare matematisk grund
De vardagliga föremålen i vår omgivning byggs alla upp av atomer, vilka består av elektroner och atomkärnor. Inuti atomkärnorna återfinns protoner och neutroner, vilka i sin tur är uppbyggda av kvarkar. För att studera materien på denna innersta nivå krävs stora acceleratorer. Sådana konstruerades först på 1950-talet och innebar då den moderna partikelfysikens födelse. För första gången kunde forskarna på ett kontrollerbart sätt låta energirika atomära partiklar krocka. Därigenom kunde man dels studera uppkomsten av nya partiklar, dels vilka krafter som verkar mellan dem.
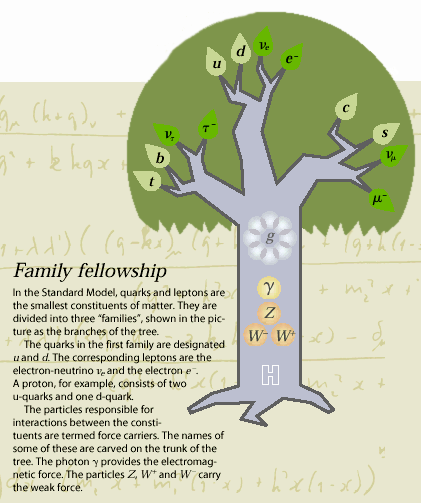
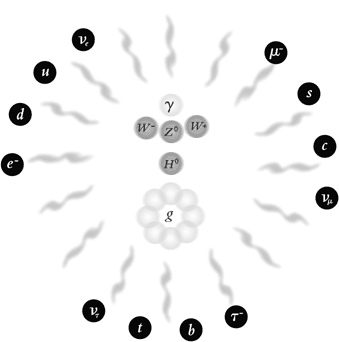
Omkring mitten av 1950-talet formulerades också en första version av den moderna teori, vilken efter många års bearbetning nu gett upphov till standardmodellen inom partikelfysiken. Enligt denna modell grupperas alla elementarpartiklar i tre familjer av kvarkar och leptoner, vilka växelverkar med hjälp av ett antal utbytespartiklar för de starka och elektrosvaga krafterna (se Figur 1).
Standardmodellens teoretiska fundament var från början ofullständigt ur matematisk synpunkt och det var framförallt oklart om teorin överhuvudtaget skulle kunna användas för detaljerade beräkningar av fysikaliska storheter. Gerardus ‘t Hooft och Martinus J.G. Veltman Nobelprisbelönas i år för att ha satt denna teori på fastare matematisk grund. Därmed har forskarna nu även fått ett väl fungerande “teoretiskt maskineri”, vilket bl.a. kan användas för att förutsäga egenskaper hos nya partiklar.
 |
|
Figur 1. Materiens fundamentala partiklar är sex leptoner och sex kvarkar. Inom partikelfysikens standardmodell beskrivs krafterna mellan dem av kvantfältteorier som alla är av typ icke-abelska gaugeteorier. Den elektrosvaga kraften förmedlas av fyra utbytespartiklar. Dessa är den masslösa fotonen (gamma) och de tre tunga partiklarna W+, W – och Z0. Den starka kraften förmedlas av åtta masslösa s.k. gluoner, g. Utöver dessa tolv utbytespartiklar förutsäger teorin även att det existerar en mycket tung partikel, Higgspartikeln H0, vars fält ger upphov till alla partikelmassor. |
Nytt namn på gammal teori
De moderna teorier som idag används inom partikelfysikens standardmodell och som beskriver växelverkan mellan partiklar är alla s.k. gaugeteorier. Namnet gauge (som i engelskan bl.a. kan betyda måttstock ) syftar på en speciell egenskap hos dessa teorier, gaugesymmetri, vilken av många forskare betraktas som en av fysikens mest fundamentala egenskaper. Men redan på 1860-talet formulerade skotten James Clerk Maxwell en teori för elektromagnetism som med dagens moderna terminologi är en gaugeteori. Hans teori, som står sig än idag, förenade elektricitet med magnetism och förutsade bl.a. existensen av radiovågor.
Man kan åskådliggöra begreppet gaugesymmetri på följande sätt: Elektriska och magnetiska fält kan uttryckas med hjälp av potentialfunktioner. Dessa kan bytas ut (gaugetransformeras) enligt ett visst schema utan att fälten därför ändrar sig. Den allra enklaste transformationen är att addera en konstant till den elektriska potentialen. Fysikaliskt illustrerar detta det välkända faktum att den elektriska potentialen kan räknas från en godtycklig nollpunkt, endast skillnader i potential spelar någon roll. Det är därför som en ekorre kan promenera på en högspänningsledning utan att ta skada! Att nollpunkten kan flyttas på detta sätt uppfattas av fysikerna som en symmetri hos teorin, gaugesymmetri.
Det visar sig att om man utför två gaugetransformationer efter varandra så spelar det ingen roll i vilken ordning man tar dem. Detta brukar uttryckas så att elektromagnetismen är en abelsk gaugeteori, efter den norske matematikern Niels Henrik Abel, som levde 1802-29. (Ett enkelt exempel på transformationer som är abelska är rotationer i planet. Pröva själv med en penna! Se Figur 2a)
Figur 2a) Ett exempel på en grupp abelska transformationer är rotationerna i ett två-dimensionellt plan.
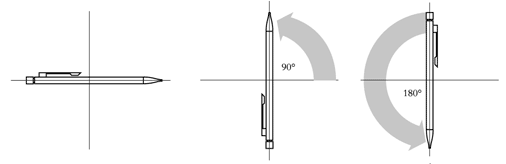
|
Lägg en penna på ett bord. |
Vrid den först 90o… |
därefter 180o åt samma håll. |
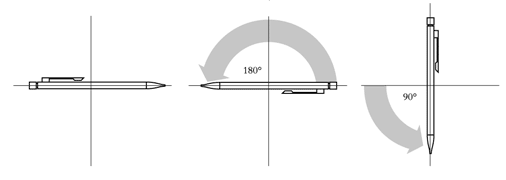
|
Kasta nu om ordningsföljden: |
Vrid först 180o… |
och sedan 90o. Resultatet är detsamma! |
Figur 2b) Ett exempel på en grupp icke-abelska transformationer är rotationer i det tre-dimensionella rummet.
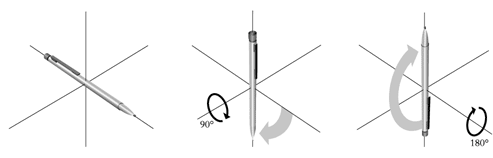
|
Håll först en penna horisontellt med spetsen åt höger |
Vrid den 90° så att spetsen pekar mot golvet. |
Vrid den därefter 180° så att spetsen pekar uppåt. |
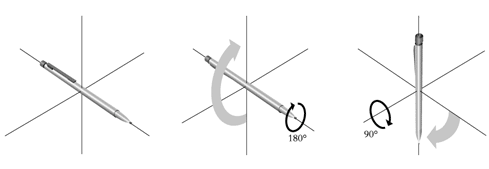
|
Lägg nu pennan i samma startläge som tidigare, men kasta om ordningsföljden på vridningarna. |
Utför först 180°-vridningen (vilken inte ändrar spetsens riktning, men får pennan att snurra ett halvt varv). |
Utför därefter 90°-vridningen (vilken får spetsen att peka mot golvet). Resultatet är nu helt annorlunda! |
Kvantmekaniken ställer till problem
Direkt efter det att kvantmekaniken formulerats omkring 1925 gjordes försök att förena kvantmekanikens vågfunktioner och elektromagnetismens fält till en kvantfältteori. Men då stötte man på problem! Den nya kvantelektrodynamiken blev komplicerad och då man ville utföra beräkningar blev många resultat orimliga. En anledning var att kvantteorin förutsäger att det elektromagnetiska fältet i närheten av t.ex. en elektron eller en proton spontant kan ge upphov till mängder av mycket kortlivade par av partiklar och antipartiklar, virtuella partiklar (se Figur 3). Ett system med endast en elektron blev plötsligt ett mångpartikelproblem!
Problemen löstes på 1940-talet av Sin-Itiro Tomonaga, Julian Schwinger och Richard P. Feynman (som fick dela 1965 års Nobelpris för sina insatser). Den metod dessa tre utvecklade kallas renormering och kan enkelt sägas innebära att man betraktar de enstaka partiklarna “lite på avstånd”. Därigenom behöver man inte ta hänsyn till de virtuella partikelparen individuellt utan kan låta “molnet” av virtuella partikelpar skymma den centrala, ursprungliga partikeln. Denna erhåller på så sätt bl.a. en ny laddning och en ny massa. I modern terminologi kan det sägas att Tomonaga, Schwinger och Feynman renormerade en abelsk gaugeteori.
Kvantelektrodynamiken har på senare tid testats med större noggrannhet än någon annan fysikalisk teori. Så har t.ex. Hans Dehmelt (Nobelpris i fysik 1989) i en jonfälla lyckats mäta elektronens magnetism med 12 siffrors noggrannhet. De första 10 siffrorna kunde jämföras med beräknade resultat och stämde då direkt!
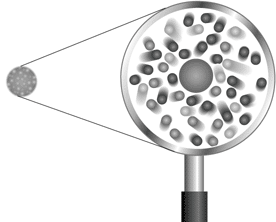
Figur 3. Enligt kvantfältteorin består en verklig “fysikalisk” partikel av en “naken” centralpartikel “påklädd” av ett moln av mycket kortlivade s.k. virtuella partiklar.
Förenad elektromagnetisk och svag växelverkan
Upptäckten och studiet av radioaktivitet och den senare utvecklingen av kärnfysiken gav under 1900-talets första hälft bl.a. upphov till begreppen stark och svag växelverkan. Enkelt uttryckt håller den starka ihop atomkärnan medan den svaga låter vissa atomkärnor sönderfalla radioaktivt. Redan på 1930-talet formulerades en första kvantfältteori för svag växelverkan. Denna teori led av problem som var ännu värre än de som kvantelektro-dynamiken haft och inte ens den renormeringsmetod som Tomonaga, Schwinger och Feynman utvecklat kunde lösa problemen.
Men i mitten av 1950-talet fann forskarna Chen Ning Yang och Robert L. Mills ett första exempel på en kvantfältteori med nya egenskaper, en icke-abelsk gaugeteori. Till skillnad från den abelska varianten, i vilken gaugetransformationer kan utföras oberoende av ordningsföljd, beror resultaten i den icke-abelska av ordningsföjden. Detta ger teorin en mer komplicerad matematisk struktur, men öppnar också nya möjligheter. (Ett enkelt exempel på transformationer som är icke-abelska är rotationer i rummet. Pröva själv med en penna! Se Figur 2b.)
Teorins nya möjligheter utnyttjades till fullo först på 1960-talet, då en rad forskare medverkade i utvecklandet av en icke-abelsk gaugeteori som förenar elektromagnetisk och svag växelverkan till en elektrosvag växelverkan (Nobelpris 1979 till Sheldon L. Glashow, Abdus Salam och Steven Weinberg). Denna kvantfältteori förutsade bl.a. de nya partiklarna W och Z, vilka 1983 påvisades vid det europeiska accelerator-laboratoriet CERN i Genève (Nobelpris 1984 till Carlo Rubbia och Simon van der Meer).
Historien upprepar sig
Teorin för elektrosvag växelverkan som utvecklades på 1960-talet var visserligen ett stort steg framåt, men forskarsamhället hade först svårt att acceptera den. Då man ville använda teorin för att beräkna närmare egenskaper hos de nya partiklarna W och Z (och många andra fysikaliska storheter) gav den orimliga resultat. Situationen liknande den på 1930-talet, innan Tomonaga, Schwinger och Feynman lyckats renormera kvantelektro-dynamiken. Många forskare var pessimistiska om möjligheterna att komma vidare med en sådan teori.
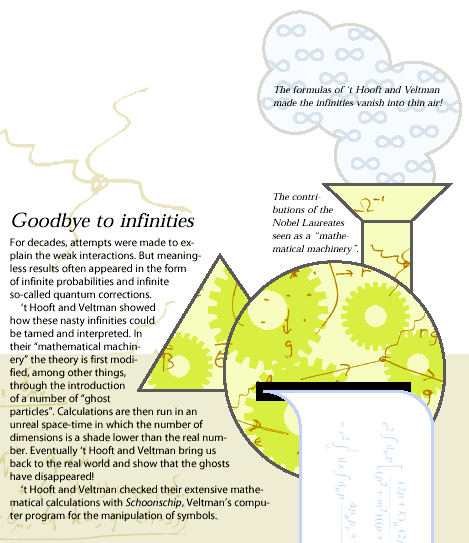
En som inte gett upp hoppet om att kunna renormera icke-abelska gaugeteorier var Martinus J.G. Veltman. Han var i slutet av 1960-talet nyutnämnd professor vid universitet i Utrecht. Veltman hade utvecklat ett datorprogram Schoonschip som symboliskt utförde algebraiska förenklingar av de komplicerade uttryck som alla kvantfältteorier resulterar i då man vill göra kvantitativa beräkningar. 20 år tidigare hade visserligen Feynman systematiserat beräkningsproblemet och infört s.k. Feynmandiagram, vilka snabbt accepterats inom forskarvärlden. Men på den tiden fanns inga datorer. Veltman trodde benhårt på möjligheten att hitta ett sätt att utföra renormeringen, och hans datorprogram var en hörnsten i det omfattande arbetet att testa olika idéer.
På våren 1969 fick Veltman en ung 22-årig elev, Gerardus ‘t Hooft, som hade uttryckt önskemål om att få studera högenergifysik. Efter att ha skrivit en första mindre avhandling antogs ‘t Hooft som doktorand samma höst. Uppgiften var att medverka i sökandet efter en metod att renormera icke-abelska gaugeteorier. ‘t Hooft lyckades över all förväntan och publicerade redan 1971 två artiklar som representerade ett viktigt genombrott i forskningsprogrammet.
Med hjälp av Veltmans datorprogram verifierades nu ‘t Hoofts delresultat och gemensamt utarbetade de en fungerande beräkningsmetod i detalj. Därmed hade den elektrosvaga växelverkans icke-abelska gaugeteori blivit ett fungerande teoretiskt maskineri och man kunde, precis som för kvantelektrodynamiken 20 år tidigare, börja göra precisa beräkningar.
Teorins utsagor verifieras
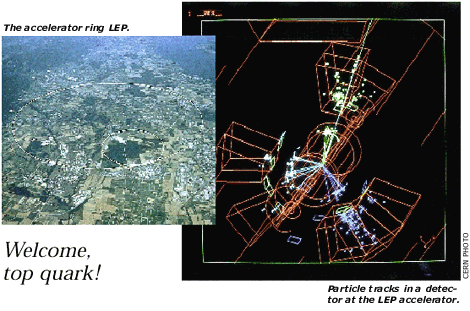
Som redan beskrivits ovan förutsade den elektrosvaga teorin redan från början existensen av de nya partiklarna W och Z. Men först genom ‘t Hoofts och Veltmans arbeten kunde man mer precist börja beräkna fysikaliska storheter i vilka egenskaperna hos W och Z spelar in. I acceleratorn LEP vid CERN har man på senare tid lyckats skapa stora mängder W och Z under kontrollerbara förhållanden. Jämförelser mellan mätningar och beräkningar har hela tiden visat stor överensstämmelse och styrker därmed teorins utsagor.
En speciell kvantitet som kunde erhållas med ‘t Hoofts och Veltmans beräkningsmetod utgående från resultaten vid LEP är massan hos den s.k. toppkvarken, den tyngsta av de två kvarkar som ingår i standardmodellens tredje familj. Denna kvark iakttogs direkt för första gången 1995, vid Fermilab i USA, men dess massa hade förutsagts redan flera år tidigare. Överensstämmelsen mellan experiment och teori var även här tillfredsställande.
När kommer nästa stora upptäckt?
En viktig ingrediens i den teori som ‘t Hooft och Veltman utvecklat är en ännu ej påvisad partikel, den s.k. Higgspartikeln (se Figur 1). På samma sätt som andra partiklar har förutsagts av teoretiska argument för att senare påvisas experimentellt väntar nu forskarna på den direkta observationen av Higgspartikeln. Genom beräkningar, liknande dem för toppkvarkens massa, vet man att det finns en chans att en av de nuvarande acceleratorerna kan förmås att producera några Higgspartiklar. Men den enda accelerator som är under konstruktion idag och som kommer att vara tillräckligt kraftfull för närmare studier av den nya partikeln är LHC (Large Hadron Collider) vid CERN. Men med den får forskarna ge sig till tåls några år till, eftersom LHC beräknas vara färdigställd först år 2005!
| Lästips |
| Additional background material on the Nobel Prizes in Physics 1999, by Professor Cecilia Jarlskog, the Royal Swedish Academy of Sciences (pdf). |
| In search of the Ultimate Building Blocks by Gerard ‘t Hooft, Cambridge University Press 1997. |
| The Higgs boson by Martinus J.G. Veltman, Scientific American, November 1986, p. 88. |
| An Elementary Primer for Gauge Theory by K. Moriyasu, World Scientific Publishing 1983. |
| Gauge Theories of the Forces between Elementary Particles by Gerard ‘t Hooft, Scientific American, June 1980, p. 90. |
| Fyra naturkrafter blir tre – 1979 års nobelpris i fysik av Cecilia Jarlskog och Bengt E.Y. Svensson. I Svenska Fysikersamfundets årsbok Kosmos 1980. |
| Tredelat fysikpris för arbete med elementarpartiklar. Kungl. Vetenskapsakademiens pressmeddelande 1979 |
| 1965 års nobelpris i fysik av Gunnar Källén. I Svenska Fysikersamfundets årsbok Kosmos 1965. |
| Flera uppslagsord i Nationalencyklopedin, bl.a.: elementarpartikel (av Jan S. Nilsson, som där kallar gaugetransformation för skaltransformation) elektrosvag växelverkan (av Jan S. Nilsson) gauge (av Cecilia Jarlskog) Higgspartikel ‘t Hooft, Gerardus |
Gerardus ‘t Hooft
född 1946 i Den Helder, Nederländerna. Holländsk medborgare. Doktorsgrad i fysik 1972 vid universitetet i Utrecht. Professor i fysik vid universitetet i Utrecht sedan 1977. ‘t Hooft har bl.a. erhållit Dannie Heineman Prize av American Physical Society 1979 och Wolfpriset 1982 för sina arbeten rörande renormering av gaugeteorier. Han är ledamot av den holländska vetenskapsakademien sedan 1982.
Professor Gerardus ‘t Hooft
Spinoza Instituut
Leuvenlaan 4
Postbus 80.195
3508 TD Utrecht
The Netherlands
Martinus J.G. Veltman
född 1931 i Nederländerna. Holländsk medborgare. Doktorsgrad i fysik 1963 vid universitetet i Utrecht. Professor i fysik vid universitetet i Utrecht 1966-81 och vid University of Michigan, Ann Arbor, från 1981 (nu pensionerad). Veltman har bl.a. erhållit 1993 års High Energy and Particle Physics Prize av European Physical Society för sina arbeten rörande renormering av gaugeteorier. Han är ledamot av den holländska vetenskapsakademien sedan 1981.
Professor Martinus J. G. Veltman
Schubertlaan 15
3723 LM Bilthoven
The Netherlands
Prissumman uppgår 1999 till SEK 7,9 miljoner.
Pressemitteilung: Der Nobelpreis in Physik 1999
English
German
French
Swedish

12 Oktober 1999
Die Königlich Schwedische Akademie der Wissenschaften hat den Nobelpreis in Physik für das Jahr 1999 gemeinsam verliehen an
Professor Gerardus ‘t Hooft, Utrecht Universität, Utrecht, Niederlande, und
Professor emeritus Martinus J.G. Veltman, Michigan Universität, USA, ansäßig in Bilthoven, Niederlande.
Die beiden Forscher erhalten den Nobelpreis dafür, daß sie die Theorie der Elementarteilchenphysik auf festeren mathematischen Grund gestellt haben. Sie haben im speziellen gezeigt, wie die Theorie zu genauen Berechnungen physikalischer Grössen angewendet werden kann. Experimente an den Teilchenbeschleunigerlaboratorien in Europa und den USA haben kürzlich viele der berechneten Ergebnisse bestätigt.
Entscheidung der Akademie der Wissenschaften:
“für ihre entscheidenden, die Quantenstruktur betreffenden Beiträge zur Theorie der elektroschwachen Wechselwirkung in der Physik”.
Die Theorie der Elementarteilchenphysik auf festerem mathematischen Grund
Die alltäglichen Gegenstände in unserer Umgebung sind alle aus Atomen, die aus Elektronen und Atomkernen bestehen, aufgebaut. Innerhalb der Atomkerne befinden sich Protonen und Neutronen, die wiederum aus Quarks aufgebaut sind. Um die Materie auf diesem innersten Niveau zu studieren, benötigt man große Beschleuniger. Diese wurden erst in den 50er Jahren gebaut und das bedeutete die Geburt der modernen Elementarteilchenphysik. Zum ersten Mal konnten die Forscher energiereiche atomare Partikel kontrollierbar zusammenstoßen lassen. Dadurch konnte man sowohl das Entstehen neuer Teilchen als auch die Beschaffenheit der Kräfte, die zwischen ihnen wirken, studieren.
Ungefähr in der Mitte der 50er Jahre wurde auch die erste Fassung einer modernen Theorie formuliert, die nach vielen Jahren der Bearbeitung nun zu dem Standardmodell in der Elementarteilchenphysik Anlaß gegeben hat. Gemäß diesem Modell werden alle Elementarteilchen in drei Familien von Quarks und Leptonen eingeteilt, welche mit Hilfe von einer Anzahl von Austauschteilchen für die starken und elektroschwachen Kräfte wechselwirken. (Siehe Abb. 1) Das theoretische Fundament des Standardmodells war aus mathematischem Gesichtspunkt von Anfang an unvollständig und es war vor allem unklar, ob die Theorie überhaupt zu detaillierten Berechnungen physikalischer Größen verwendet werden könnte. In diesem Jahr werden Gerardus ‘t Hooft und Martinus J.G. Veltman dafür mit dem Nobelpreis ausgezeichnet, daß sie diese Theorie auf festeren mathematischen Grund gestellt haben. Dadurch haben die Forscher nun auch eine gut funktionierende “theoretische Maschinerie”, die unter anderem zur Vorhersage von Eigenschaften neuer Teilchen verwendet werden kann.
 |
|
Abb. 1 Die fundamentalen Teilchen der Materie sind sechs Leptonen und sechs Quarks. In dem Standardmodell der Teilchenphysik werden die Kräfte zwischen diesen durch Quantenfeldtheorien beschrieben, die alle vom Typ nicht-abelscher Eichtheorien sind. Die elektroschwache Kraft wird von vier Austauschteilchen übertragen. Das sind die masselosen Photonen (gamma) und die drei schweren Teilchen W+, W – und Z0. Die starke Kraft wird von acht masselosen sogenannten Gluonen g übertragen. Die Theorie sagt voraus, daß es über diese zwölf Austauschteilchen hinaus ein sehr schweres Teilchen, das Higgs-Teilchen H0, gibt, dessen Feld alle diese vielen Teilchen verursacht |
Neuer Name für alte Theorie
Die heute in dem Standardmodell der Elementarteilchenphysik verwendeten modernen Theorien, welche die Wechselwirkung zwischen den Teilchen beschreiben, sind alle sogenannte Eichtheorien. Der Name bezieht sich auf eine spezielle Eigenschaft dieser Theorien, die Eichsymmetrie, die von vielen Forschern als eine der fundamentalsten Eigenschaften der Physik angesehen wird. Aber schon um 1860 formulierte der Schotte James Clerk Maxwell eine Theorie für den Elektromagnetismus, die in heutiger, moderner Terminologie eine Eichtheorie ist. Seine Theorie, die auch heute noch Gültigkeit besitzt, vereinte Elektrizität mit Magnetismus und sagte unter anderem die Existenz von Radiowellen voraus.
Man kann den Begriff Eichsymmetrie auf folgende Art anschaulich machen: Elektrische und magnetische Felder können mit Hilfe von Potentialfunktionen dargestellt werden. Diese Funktionen können nach einem gewissen Schema ausgetauscht (eichtransformiert) werden ohne daß sich die Felder deswegen ändern. Die allereinfachste Transformation ist die Addition einer Konstanten zu den elektrischen Potentialen. Physikalisch verdeutlicht dieses die wohlbekannte Tatsache, daß das elektrische Potential von einem willkürlichen Nullpunkt aus gerechnet werden kann; nur Änderungen im Potential spielen eine Rolle. Deshalb kann ein Eichhörnchen auf einer Hochspannungsleitung entlang laufen ohne Schaden zu nehmen. Die Möglichkeit einer derartigen Verschiebung des Nullpunkts wird von den Physikern als eine Symmetrie in der Theorie, eine Eichsymmetrie, aufgefaßt.
Es zeigt sich, daß es bei der Ausführung von zwei Eichtransformationen nacheinander keine Rolle spielt, in welcher Reihenfolge man vorgeht. Deshalb pflegt man den Elektromagnetismus als eine abelsche Eichtheorie zu bezeichnen nach dem norwegischen Mathematiker Niels Henrik Abel, der von 1802 bis 1829 lebte. (Ein einfaches Beispiel für Transformationen, die abelsch sind, sind Drehungen in der Ebene. Versuchen Sie selbst mit einem Bleistift! Siehe Abb. 2).
Abb. 2a) Ein Beispiel für eine Gruppe abelscher Transformationen sind die Drehungen in einer zweidimensionalen Ebene.

|
Legen Sie einen Bleistift auf einen Tisch. |
Drehen ihn zuerst um 90o… |
und dann um 180o in dieselbe Richtung |

|
Vertauschen Sie nun die Reihenfolge: |
Drehen zuerst um 180o |
und dann um 90o. Das Ergebnis ist dasselbe! |
Abb. 2b) Ein Beispiel für eine Gruppe nicht-abelscher Transformationen sind Drehungen im dreidimensionalen Raum.

|
Halten Sie zuerst einen Bleistift horizontal mit der Spitze nach rechts. |
Drehen Sie ihn um 90o, so daß die Spitze zum Boden zeigt. |
Drehen Sie sodann um 180o, so daß die Spitze nach oben zeigt. |

|
Vertauschen Sie nun die Reihenfolge |
Drehen Sie zuerst um 180o (was nicht die Richtung der Spitze ver-ändert, sondern den Bleistift eine halbe Umdrehung rotieren läßt). |
Führen Sie nun die 90o Drehung aus (welche die Spitze zu Boden zeigen läßt). Das Ergebnis ist nun ganz anders! |
Vereinigte elektromagnetische und schwache Wechselwirkung
Die Entdeckung und das Studium der Radioaktivität und die spätere Entwicklung der Kernphysik gab in der ersten Hälfte des 20sten Jahrhunderts Anlaß zu Begriffen wie starke und schwache Wechselwirkung. Einfach ausgedrückt hält die starke die Atomkerne zusammen, während die schwache gewisse Atomkerne radioaktiv zerfallen läßt. Schon in den 30er Jahren wurde eine erste Quantenfeldtheorie für schwache Wechselwirkung formuliert. Diese Theorie litt unter Problemen die noch schlimmer waren als diejenigen, die die Quantenelektrodynamik hatte und nicht einmal die von Tomonaga, Schwinger und Feynman entwickelte Renormierungsmethode konnte die Probleme lösen.
Aber in der Mitte der 50er Jahre fanden einige Forscher ein erstes Beispiel für eine Quantenfeldtheorie mit neuen Eigenschaften, eine nicht-abelsche Eichtheorie. Zum Unterschied von der abelschen Variante, in welcher Eichtransformationen unabhängig von der Reihenfolge ausgeführt werden können, beruhen die Ergebnisse in der nicht-abelschen auf der Reihenfolge. Das gibt der Theorie eine kompliziertere mathematische Struktur, aber eröffnet auch neue Möglichkeiten. (Ein einfaches Beispiel für Transformationen, die nicht-abelsch sind, sind Drehungen im Raum. Versuchen Sie selbst mit einem Bleistift! Siehe Abb. 2b.)
Die neuen Möglichkeiten der Theorie wurden erst in den 60er Jahren voll genutzt, als eine Reihe von Forschern bei der Entwicklung einer nicht-abelschen Eichtheorie mitwirkten, welche die elektromagnetische mit der schwachen Wechselwirkung zu einer elektroschwachen Wechselwirkung vereinigt (Nobelpreis 1979 für Sheldon L. Glashow, Abdus Salam und Steven Weinberg). Diese Quantenfeldtheorie sagte unter anderem die neuen Teilchen W und Z voraus, die 1983 am europäischen Beschleunigerlabor CERN, Genf (Nobelpreis 1984 für Carlo Rubbia und Simon van der Meer) nachgewiesen wurden.

Abb.3 Gemäß der Quantenfeldtheorie besteht ein richtiges “physikalisches” Teilchen aus einem “nackten” Zentralteilchen “angezogen” mit einer Wolke von vielen kurzlebigen, sogenannten virutellen Teilchen.
Die Quantenelektrodynamik ist in letzter Zeit mit größerer Sorgfalt als irgendeine andere physikalische Theorie geprüft worden. So ist es z.B. Hans Dehmelt (Nobelpreis in Physik 1989) gelungen, in einer Ionenfalle den Magnetismus des Elektrons mit einer Genauigkeit von 12 Ziffern zu messen. Die ersten 10 Ziffern konnten mit dem berechneten Ergebnis verglichen werden und sie stimmten überein.
Vereinigte elektromagnetische und schwache Wechselwirkung
Die Entdeckung und das Studium der Radioaktivität und die spätere Entwicklung der Kernphysik gab in der ersten Hälfte des 20sten Jahrhunderts Anlaß zu Begriffen wie starke und schwache Wechselwirkung. Einfach ausgedrückt hält die starke die Atomkerne zusammen, während die schwache gewisse Atomkerne radioaktiv zerfallen läßt. Schon in den 30er Jahren wurde eine erste Quantenfeldtheorie für schwache Wechselwirkung formuliert. Diese Theorie litt unter Problemen die noch schlimmer waren als diejenigen, die die Quantenelektrodynamik hatte und nicht einmal die von Tomonaga, Schwinger und Feynman entwickelte Renormierungsmethode konnte die Probleme lösen.
Aber in der Mitte der 50er Jahre fanden einige Forscher ein erstes Beispiel für eine Quantenfeldtheorie mit neuen Eigenschaften, eine nicht-abelsche Eichtheorie. Zum Unterschied von der abelschen Variante, in welcher Eichtransformationen unabhängig von der Reihenfolge ausgeführt werden können, beruhen die Ergebnisse in der nicht-abelschen auf der Reihenfolge. Das gibt der Theorie eine kompliziertere mathematische Struktur, aber eröffnet auch neue Möglichkeiten. (Ein einfaches Beispiel für Transformationen, die nicht-abelsch sind, sind Drehungen im Raum. Versuchen Sie selbst mit einem Bleistift! Siehe Abb. 2b.)
Die neuen Möglichkeiten der Theorie wurden erst in den 60er Jahren voll genutzt, als eine Reihe von Forschern bei der Entwicklung einer nicht-abelschen Eichtheorie mitwirkten, welche die elektromagnetische mit der schwachen Wechselwirkung zu einer elektroschwachen Wechselwirkung vereinigt (Nobelpreis 1979 für Sheldon L. Glashow, Abdus Salam und Steven Weinberg). Diese Quantenfeldtheorie sagte unter anderem die neuen Teilchen W und Z voraus, die 1983 am europäischen Beschleunigerlabor CERN, Genf (Nobelpreis 1984 für Carlo Rubbia und Simon van der Meer) nachgewiesen wurden.
Die Geschichte wiederholt sich
Die Theorie der elektroschwachen Wechselwirkung, die in den 60er Jahren entwickelt wurde, war sicherlich ein großer Schritt vorwärts, aber die Wissenschaftler hatten es zuerst schwer, sie zu akzeptieren. Als man die Theorie zur Berechnung näherer Eigenschaften der neuen Teilchen W und Z (und vieler anderer physikalischer Größen) anwenden wollte, lieferte sie sinnlose Ergebnisse. Die Situation war der in den 30er Jahren ähnlich, bevor es Tomonaga, Schwinger und Feynman gelang, die Quantenelektrodynamik zu renormieren. Viele Forscher waren pessimistisch über die Möglichkeiten, mit einer derartigen Theorie weiterzukommen.
Einer, der nicht die Hoffnung aufgegeben hatte, nicht-abelsche Eichtheorien renormieren zu können, war Martinus J.G. Veltman. Er war zu Ende der 60er Jahre neu ernannter Professor an der Universität in Utrecht. Veltman hatte ein Computerprogramm Schoonschip entwickelt, welches symbolisch algebraische Vereinfachungen der komplizierten Ausdrücke durchführte, die sich in allen Quantenfeldtheorien bei quantitativen Berechnungen ergeben. 20 Jahre früher hatte zwar Feynman das Berechnungsproblem systematisiert und die sogenannten Feynmandiagramme, die schnell in der Welt der Forschung angenommen wurden, eingeführt; aber damals gab es keine Computer. Veltman glaubte felsenfest an die Möglichkeit, einen Weg zu finden, um die Renormierung auszuführen, und sein Computerprogramm war ein Meilenstein in der umfangreichen Arbeit, verschiedene Ideen auszutesten.
Im Frühjahr 1969 bekam Veltman einen jungen, 22 Jahre alten Schüler, Gerardus ‘t Hooft, der seinen Wunsch ausgedrückt hatte, Hochenergiephysik studieren zu dürfen. Nachdem er eine erste kleine Abhandlung geschrieben hatte wurde ‘t Hooft im Herbst des gleichen Jahres als Doktorand angenommen. Die Aufgabe war, bei der Suche nach einer Methode zur Renormierung nicht-abelscher Eichtheorien mitzuarbeiten. Er war überaus erfolgreich und veröffentlichte schon 1971 zwei Arbeiten, die einen wichtigen Durchbruch im Forschungsprogramm darstellten.
Mit Hilfe von Veltmans Computerprogramm wurde nun ‘t Hoofts Teilergebnis bestätigt und gemeinsam arbeiteten sie eine funktionierende Berechnungsmethode im Detail aus. Somit war die nicht-abelsche Eichtheorie der elektroschwachen Wechselwirkung eine funktionierende theoretische Maschinerie geworden und man konnte, genau wie vor 20 Jahren, mit genauen Berechnungen beginnen.
Die Aussagen der Theorie werden bestätigt
Wie schon oben dargestellt, sagte die elektroschwache Theorie schon von Anfang an die Existenz der neuen Teilchen W und Z voraus. Aber erst durch ‘t Hoofts und Veltmans Arbeiten konnte man beginnen, physikalische Größen, bei denen die Eigenschaften von W und Z eine Rolle spielen, genauer zu berechnen. In dem Beschleuniger LEP bei CERN ist es in letzter Zeit gelungen, große Mengen von W und Z unter kontrollierbaren Verhältnissen zu erzeugen. Vergleiche zwischen Messungen und Rechnungen haben immer große Übereinstimmung gezeigt und sie stärken dadurch die Aussagen der Theorie.
Eine spezielle Größe, die ausgehend von den Ergebnissen am LEP mit ‘t Hoofts und Veltmans Berechnungsmethode erhalten werden konnte, ist die Masse des sogenannten top-Quarks, des schwersten der beiden Quarks, die zu der dritten Familie des Standardmodells gehören. Dieses Quark wurde zum ersten Mal direkt 1995 an dem Fermilabor in den USA beobachtet, aber seine Masse war schon einige Jahre früher vorhergesagt worden. Die Übereinstimmung zwischen Experiment und Theorie war auch hier zufriedenstellend.
Wann kommt die nächste große Entdeckung?
Ein wichtiger Bestandteil in der Theorie, die ‘t Hooft und Veltman entwickelt haben, ist ein noch nicht nachgewiesenes Teilchen, das Higgs-Teilchen (Siehe Abb. 1). Ebenso, wie andere Teilchen durch theoretische Beweisführung vorausgesagt wurden, um dann später experimentell nachgewiesen zu werden, warten die Forscher nun auf die direkte Beobachtung des Higgs-Teilchens. Durch Berechnungen, ähnlich denen für die Masse des top-Quarks, weiß man, daß vielleicht einer der zur Zeit arbeitenden Beschleuniger einige Higgs-Teilchen erzeugen kann. Aber der einzige Beschleuniger, der ausreichende Leistung für genauere Studien haben wird, ist der zur Zeit im Bau befindliche LHC (Large Hadron Collider ) bei CERN. Jedoch damit müssen sich die Forscher noch einige Jahre gedulden, denn der LHC wird voraussichtlich erst im Jahr 2005 fertiggestellt sein.
| Lektürehinweise |
| Additional background material on the Nobel Prizes in Physics 1999, by Professor Cecilia Jarlskog, the Royal Swedish Academy of Sciences (pdf). |
| In search of the Ultimate Building Blocks by Gerard ‘t Hooft, Cambridge University Press 1997. |
| The Higgs boson by Martinus J.G. Veltman, Scientific American, November 1986, p. 88. |
| An Elementary Primer for Gauge Theory by K. Moriyasu, World Scientific Publishing 1983. |
| Gauge Theories of the Forces between Elementary Particles by Gerard ‘t Hooft, Scientific American, June 1980, p. 90. |
Gerardus ‘t Hooft
geboren 1946 in Den Helder, Niederlande. Bürger der Niederlande. Zum Doktor der Physik promoviert 1972 an der Universität in Utrecht. Professor für Physik an der Universität in Utrecht seit 1977. ‘t Hooft hat unter anderem 1979 den Dannie Heineman Preis von der American Physical Society und 1982 den Wolfspreis für seine Arbeiten über die Renormierung von Eichtheorien erhalten. Er ist Mitglied der Holländischen Akademie der Wissenschaften seit 1982.
Professor Gerardus ‘t Hooft
Spinoza Instituut
Leuvenlaan 4
Postbus 80.195
3508 TD Utrecht
The Netherlands
Martinus J.G. Veltman
geboren 1931 in den Niederlanden. Bürger der Niederlande. Zum Doktor der Physik promoviert 1963 an der Universität in Utrecht. Professor für Physik an der Universität in Utrecht 1966 – 1981 und an der Universität von Michigan, Ann Arbor, seit 1981 (jetzt pensioniert). Veltman hat unter anderem den Hochenergie- und Elementarteilchen-Physikpreis des Jahres 1983 von der Europäischen Physikalischen Gesellschaft für seine Arbeiten über die Renormierung von Eichtheorien erhalten. Er ist Mitglied der Holländischen Akademie der Wissenschaften seit 1981.
Professor Martinus J. G. Veltman
Schubertlaan 15
3723 LM Bilthoven
The Netherlands
Die Preissumme des diesjährigen Nobelpreises in Physik beträgt SEK 7 900 000.
Communiqué de presse: Le Prix Nobel de Physique de 1999
English
German
French
Swedish

12 Octobre 1999
L’Académie Royal des Sciences de Suède a attribué le Prix Nobel de Physique de l’année 1999 collectivement aux
Professeur Gerardus ‘t Hooft, Université d’Utrecht, Utrecht, Pays-Bas, et
Professeur émérite Martinus J.G. Veltman de University of Michigan, États-Unis, domicilié à Bilthoven, Pays-Bas.
Les deux chercheurs reçoivent le Prix Nobel pour avoir fourni à la théorie de la physique des particules une base mathématique plus solide. Il ont notamment montré comment utiliser la théorie pour préciser les calculs de grandeurs physiques mesurables. Des expériences dans les accélérateurs de particules en Europe et aux Etats-Unis ont récemment confirmé de nombreux résultats calculés.
Motivation de l’Académie des Sciences:
«pour leur travaux déterminants sur la structure quantique dans la théorie d’interaction électrofaible de la physique»
Théorie de la physique des particules sur une base mathématique plus solide
Les objets de notre environnement quotidien sont tous constitués d’atomes, eux-mêmes constitués d’électrons et de noyaux atomiques. Ceux-ci sont à leur tour composés de protons et de neutrons, eux-mêmes constitués de quarks. L’étude de la matière au niveau de ces éléments internes exige des accélérateurs puissants. Les premiers remontent aux années 1950 et marquent la naissance de la physique des particules moderne. Pour la première fois, les chercheurs réussirent alors à provoquer, sous une forme contrôlée, des collisions de particules atomiques hautement énergétiques. C’est ainsi que les physiciens observèrent l’apparition de nouvelles particules et identifièrent les forces qui agissent entre elles.
C’est aussi dans les années 1950 que fut formulée une première version de la théorie moderne qui, après de nombreuses années de perfectionnement, a finalement donné naissance au modèle standard au sein de la physique des particules. Selon ce modèle, toutes les particules élémentaires, regroupées dans trois familles de quarks et de leptons, interagissent à l’aide d’un certain nombre de particules médiatrices pour les forces fortes et électrofaibles (voir Figure 1).
La base théorique du modèle standard était initialement incomplète du point de vue mathématique et il n’était même pas certain qu’elle fût applicable à des calculs détaillés sur des grandeurs physiques mesurables. Cette année, Gerardus ‘t Hooft et Martinus J.G. Veltman sont récompensés par le Prix Nobel pour avoir fourni à cette théorie mathématique une base plus solide. Les chercheurs disposent désormais d’un édifice théorique qui peut leur servir, entre autres, à prédire les propriétés des nouvelles particules.
 |
|
Fig. 1. Les particules fondamentales de la matière sont six leptons et six quarks. Dans le modèle standard de la physique des particules, les forces entre ces éléments sont décrites par des théories quantiques des champs qui toutes sont des types de théories de jauge non abéliennes. Selon celles-ci, les forces électrofaibles sont transmises par quatre particules médiatrices. Ce sont le photon de masse nulle (gamma) et les trois particules lourdes W+, W – et Z0. La force forte est transmise par huit «gluons» g de masse nulle. En plus de ces douze particules médiatrices, la théorie prédit également l’existence d’une particule de champ très lourde, la particule de Higgs H0 dont le champ engendre toutes les masses des particules. |
Nouvelle dénomination d’une ancienne théorie
Les modèles théoriques modernes exploités aujourd’hui dans le modèle standard de la physique des particules et qui décrivent l’interaction entre les particules sont appelés
théories de jauge. Le nom jauge définit une propriété spécifique chez ces théories, la symétrie de jauge, considérée par de nombreux chercheurs comme l’une des propriétés les plus fondamentales de la physique. Mais dès les années 1860, l’Ecossais James Clerk Maxwell formula une théorie applicable à l’électromagnétisme qui, selon la terminologie moderne, est une théorie de jauge. Sa théorie, encore viable aujourd’hui, unifiait l’électricité au magnétisme et prédisait, entre autres, l’existence d’ondes hertziennes.
Il est possible d’illustrer le concept de la symétrie de jauge de la façon suivante: les champs électriques et magnétiques peuvent être exprimés à l’aide de fonctions potentielles. Celles-ci peuvent être échangées (transformation de jauge) selon un certain modèle sans provoquer la modification du champ. La transformation la plus simple consiste à additionner une constante au potentiel électrique. Pour les grandeurs physiques mesurables, ceci illustre une loi bien connue. Il est possible de calculer le potentiel électrique à partir d’un point zéro de l’espace-temps choisi arbitrairement: on fait varier le potentiel de jauge sans que le champ ne subisse la moindre modification. C’est ce qui explique qu’un écureuil puisse se promener sur une ligne à haute tension, sans risquer d’être électrocuté! Pour les physiciens, le fait que le point zéro puisse être déplacé de la sorte illustre une symétrie dans la théorie: la symétrie de jauge.
Lorsque l’on effectue deux transformations de jauge successivement, l’ordre dans lequel elles sont réalisées n’a aucune importance. L’interprétation généralement donnée à ce phénomène est que l’électromagnétisme est une théorie jauge abélienne, du nom du mathématicien Niels Henrik Abel, 1802-29. (Une illustration simple des transformations abéliennes sont les rotations dans le plan. Essayons de l’illustrer à l’aide d’un crayon! Voir Figure 2a)
Fig. 2a) Les rotations dans un plan bidimensionnel constituent un exemple de groupe de transformations abéliennes.

|
Posons un crayon sur une table, |
faisons-lui d’abord effectuer une rotation de 90o |
et puis une de 180o dans le même sens. |

|
Inversons maintenant l’ordre des rotations: |
et faisons effectuer au crayon d’abord une rotation de 180o |
et faisons effectuer au crayon d’abord une rotation de 180o |
Fig. 2b) Les rotations dans l’espace tridimensionnel constituent un exemple de groupe de transformations non abéliennes.

|
Tenons d’abord un crayon à |
Faisons-lui ensuite effectuer une rotation de 90o de sorte qu’il pointe vers le sol.. |
Tournons-le ensuite de 180o afin qu’il pointe vers le haut. |

|
Inversons maintenant l’ordre des rotations: |
Effectuons d’abord la rotation à 180o (ce qui ne change pas la direction de la pointe mais pro-voque la rotation du crayon d’un demi-tour sur lui-même). |
Effectuons la rotation à 90o (le crayon pointe alors vers le sol). Le résultat est tout à fait différent! |
La mécanique quantique pose des problèmes
Dès que la mécanique quantique fut formulée dans les années 1925, les chercheurs entreprirent d’associer les fonctions ondulatoires de la mécanique quantique et le champ électromagnétique dans une théorie quantique des champs. Mais les chercheurs se heurtèrent à des difficultés! La nouvelle électrodynamique quantique se révélait complexe et quand on effectuait des calculs, les résultats obtenus étaient absurdes. Ceci était en partie dû à la théorie quantique qui prédit que le champ électromagnétique proche d’un électron ou d’un proton, par exemple, peut spontanément engendrer des myriades de paires de particules et d’antiparticules de longévité très brève, les particules virtuelles (voir Figure 3). Un système constitué d’un seul électron devenait subitement un problème relevant d’une multitude de particules.
Ce problème fut résolu dans les années 1940 par Sin-Itiro Tomonaga, Julian Schwinger et Richard P. Feynman (qui obtint le Prix Nobel en 1965 pour ses travaux). La méthode développée par ces trois chercheurs s’appelle «renormalisation». En simplifiant, on peut dire que cette approche consiste à observer les particules individuelles «à une certaine distance» Ainsi, il n’est pas nécessaire de considérer les paires de particules virtuelles individuellement : il suffit de laisser le « nuage » formé de paires de particules virtuelles ombrager la particule centrale initiale. Ainsi, celle-ci se caractérise, entre autres, par une nouvelle charge et une nouvelle masse. En utilisant la terminologie moderne, on peut dire que Tomonaga, Schwinger et Feynman renormèrent une théorie de jauge abélienne.
Ces derniers temps, les chercheurs ont testé l’électrodynamique quantique avec une précision plus grande que pour toute autre théorie sur les grandeurs physiques mesurables. Par exemple, Hans Dehmelt (Prix Nobel de Physique 1989), a réussi, dans un piège ionique, à mesurer le magnétisme de l’électron avec une précision de 12 chiffres. Les chercheurs ont comparé les 10 premiers chiffres aux résultats des calculs: la concordance était parfaite!

Fig. 3. Selon le théorie quantique des champs, une particule de grandeur physique mesurable réelle se compose d’une particule centrale «nue», enrobée d’un manteau nuageux de «particules virtuelles» de longévité très brève.
Unification des interactions électromagnétique et faible
La découverte et l’étude de la radioactivité relayées par l’évolution de la physique nucléaire au cours de la première moitié du 20e siècle, donnèrent naissance, entre autres, aux notions d’interaction forte et faible. Pour les expliquer de façon très simplifiée, on peut dire que l’interaction forte retient ensemble les éléments du noyau atomique alors que l’interaction faible permet la désintégration radioactive de certains d’entre eux. Dans les années 1930 déjà, les chercheurs formulèrent une première théorie quantique des champs pour l’interaction faible. Ce modèle théorique se heurta à des difficultés encore plus sérieuses que ceux qu’avait connu l’électrodynamique quantique. Pas même la méthode de renormalisation développée par Tomonaga, Schwinger et Feynman ne pouvait les surmonter.
Mais au milieu des années 50, plusieurs chercheurs formulèrent un premier exemple de théorie quantique des champs présentant de nouvelles propriétés : une théorie de jauge non abélienne. A la différence de la variante abélienne, selon laquelle les transformations de jauge peuvent être réalisées indépendamment de leur ordre de succession, les résultats de la théorie non abélienne dépendent de cet ordre. Ceci confère à la théorie une structure mathématique plus complexe, mais ouvre par ailleurs de nouvelles perspectives. (Les rotations dans l’espace sont un exemple simple de transformations non abéliennes. Expérimentons avec un crayon! Voir Figure 2b)
Il fallut attendre les années 1960 pour que les nouvelles possibilités offertes par la théorie soient pleinement exploitées. Plusieurs équipes de chercheurs contribuèrent alors au développement d’une théorie de jauge non abélienne qui combine l’interaction électromagnétique et l’interaction faible en une interaction électrofaible (Prix Nobel 1979 attribué à Sheldon H. Glashow, Abdus Salam et Steven Weinberg). Cette théorie quantique des champs prédisait, entre autres, l’existence des nouvelles particules W et Z. Ces dernières furent mises en évidence en 1983 au CERN, le laboratoire d’accélération de particules à Genève (Prix Nobel 1984 décerné à Carlo Rubbia et Simon van der Meer).
L’histoire se répète
La théorie de l’interaction électrofaible développée pendant les années 1960 constituait certainement un grand pas en avant mais la communauté scientifique l’accepta difficilement dans un premier temps. Lorsqu’ils tentaient de l’utiliser pour effectuer des calculs plus précis des propriétés des nouvelles particules W et Z (ainsi que de nombreuses autres grandeurs physiques mesurables), les chercheurs obtenaient des résultats absurdes. Cette situation rappelait celle des années 30, avant que Tomonoga, Schwinger et Feynman ne réussissent à renormer l’électrodynamique quantique. De nombreux chercheurs exprimaient leur pessimisme sur les perspectives offertes par cette théorie.
Martinus J.G. Veltman appartenait au nombre de physiciens espérant encore réussir à renormer les théories de jauge non abéliennes. A la fin des années 60, il venait d’être nommé professeur à l’Université d’Utrecht. Veltman avait élaboré un logiciel, Schoonschip, qui effectuait symboliquement les simplifications algébriques d’expressions complexes engendrées par toutes les théories quantiques des champs lorsque l’on entreprenait des calculs quantitatifs. 20 ans auparavant, Feynman avait bien systématisé le problème des calculs et introduit les diagrammes dit diagrammes de Feynman, très vite adoptés par le monde des chercheurs. Mais à cette époque, les ordinateurs n’existaient pas. Veltman était pleinement convaincu qu’il trouverait un moyen d’effectuer la renormalisation, et son logiciel constituait une pierre angulaire dans le vaste travail consistant à tester les différentes idées.
Au printemps 1969, Veltman accueillit un nouvel élève de 22 ans nommé Gerardus ‘t Hooft, qui avait exprimé le désir d’étudier la physique des hautes énergies. Après avoir rédigé un premier mémoire, ‘t Hooft fut admis à préparer sa thèse de doctorat l’automne de la même année. Sa tâche consistait à participer à la recherche d’une méthode pour réaliser la renormalisation des théories de jauge non abéliennes. ‘t Hooft réussit au-delà de toute espérances et publia dès 1971 deux articles représentant une percée dans le programme de recherche.
A l’aide du logiciel de Veltman, les chercheurs procédèrent à la vérification des résultats partiels de ‘t Hooft et ils développèrent ensemble une méthode de calcul détaillée fonctionnelle. Ainsi, la théorie de jauge d’interaction électrofaible non abélienne devenait maintenant un édifice théorique utilisable, qui, tout comme pour l’électrodynamique quantique 20 auparavant, allait permettre d’effectuer des calculs précis.
Vérification des postulats théoriques
Ainsi qu’il a été décrit ci-dessus, la théorie électrofaible prédisait dès son origine l’existence des nouvelles particules W et Z. Mais les travaux de Veltman et de ‘t Hooft ouvrirent la voie à des calculs de grandeurs physicales plus précises dans lesquelles les propriétés de W et Z jouaient un rôle. Dans l’accélérateur LEP du CERN, les scientifiques créent depuis une dizaine d’années d’importantes quantités de particules W et Z dans des conditions contrôlables. Les comparaisons entre les mesures et les calculs ont constamment montré une grande concordance, confirmant ainsi les postulats théoriques.
Une quantité particulière se laissait appréhender par la méthode de calcul de Veltman et de ‘t Hooft à partir des résultats obtenus au LEP: la masse du quark top, le plus lourd des deux quarks appartenant à la troisième famille du modèle standard. Ce quark fut directement identifié la première fois en 1995 au Fermilab américain, mais sa masse avait était prédite déjà plusieurs années auparavant. Là encore, la concordance entre l’expérience et la théorie donna satisfaction.
A quand la prochaine grande découverte?
Un élément important de l’édifice théorique élaborée par Veltman et ‘t Hooft est une particule non encore identifiée, baptisée particule de Higgs (voir Figure 1). Tout comme pour d’autres particules dont l’existence a été prédite par les arguments théoriques puis identifiées expérimentalement, les chercheurs attendent maintenant l’observation directe de la particule de Higgs. Par des calculs comparables à ceux effectués pour déterminer la masse du quark top, on sait qu’il y a une chance pour que l’un des accélérateurs existants produisent quelques particules de Higgs. Mais le LHC (Large Hadron Collider ) du CERN, le seul accélérateur suffisamment puissant pour permettre l’étude détaillée de la particule est actuellement en construction. Alors les chercheurs devront faire preuve d’un peu de patience car sa mise en service n’est prévue que pour l’an 2005!
| Liste d’ouvrages conseillés |
| Additional background material on the Nobel Prizes in Physics 1999, by Professor Cecilia Jarlskog, the Royal Swedish Academy of Sciences (pdf). |
| In search of the Ultimate Building Blocks by Gerard ‘t Hooft, Cambridge University Press 1997. |
| The Higgs boson by Martinus J.G. Veltman, Scientific American, November 1986, p. 88. |
| An Elementary Primer for Gauge Theory by K. Moriyasu, World Scientific Publishing 1983. |
| Gauge Theories of the Forces between Elementary Particles by Gerard ‘t Hooft, Scientific American, June 1980, p. 90. |
Gerardus ‘t Hooft
né en 1946 à Den Helder, Pays-Bas. De nationalité néerlandaise. Doctorat de physique en 1972 à l’Université d’Utrecht. Professeur de physique à l’Université d’Utrecht depuis 1977. ‘t Hooft a, entre autres, reçu le Dannie Heineman Prize de l’American Physical Society en 1979 et le prix Wolf en 1982 pour ses travaux sur la renormalisation des théories de jauge. Il est membre de l’Académie des Sciences des Pays-Bas depuis 1982.
Professor Gerardus ‘t Hooft
Spinoza Instituut
Leuvenlaan 4
Postbus 80.195
3508 TD Utrecht
The Netherlands
Martinus J. G. Veltman
Né en 1931 aux Pays-Bas. De nationalité néerlandaise. Doctorat de physique en 1963 à l’Université d’Utrecht. Professeur de physique à l’Université d’Utrecht de 1966 à 1981 puis à l’Université du Michigan, Ann Arbor à partir de 1981 (maintenant retraité). Veltman a, entre autres distinctions, reçu en 1983 le High Energy and Particle Physics Prize de l’European Physical Society pour ses études sur la renormalisation des théories de jauge. Il est membre de l’Académie des Sciences des Pays-Bas depuis 1981.
Professor Martinus J. G. Veltman
Schubertlaan 15
3723 LM Bilthoven
The Netherlands
Le montant du prix s’élève à SEK 7,900,000.
Press release
English
German
French
Swedish

12 October 1999
The Royal Swedish Academy of Sciences has awarded the 1999 Nobel Prize in Physics jointly to
Professor Gerardus ‘t Hooft, University of Utrecht, Utrecht, the Netherlands, and
Professor Emeritus Martinus J. G. Veltman, University of Michigan, USA, resident in Bilthoven, the Netherlands.
The two researchers are being awarded the Nobel Prize for having placed particle physics theory on a firmer mathematical foundation. They have in particular shown how the theory may be used for precise calculations of physical quantities. Experiments at accelerator laboratories in Europe and the USA have recently confirmed many of the calculated results.
The Academy’s citation:
“for elucidating the quantum structure of electroweak interactions in physics”
Particle physics theory on firmer mathematical foundation
The everyday objects in our surroundings are all built up of atoms, which consist of electrons and atomic nuclei. In the nuclei there are protons and neutrons, which in turn are made up of quarks. To study matter at this innermost level, large accelerators are required. Such machines were first designed in the 1950s, signifying the birth of modern particle physics. For the first time it was possible to study the creation of new particles and the forces that act between them.
Around the middle of the 1950s, a first version of the modern theory was also formulated. Many years of work have now resulted in the standard model of particle physics. This model groups all elementary particles into three families of quarks and leptons, which interact with the help of a number of exchange particles for the strong and the electro-weak forces (Fig 1).
The theoretical foundation of the standard model was at first incomplete mathematically and in particular it was unclear whether the theory could be used at all for detailed calculations of physical quantities. Gerardus ‘t Hooft and Martinus J. G. Veltman are being awarded this year’s Nobel Prize for having placed this theory on a firmer mathematical foundation. Their work has given researchers a well functioning “theoretical machinery” which can be used for, among other things, predicting the properties of new particles.
 |
| Fig. 1. Matter’s fundamental particles are six leptons and six quarks. In the standard model of particle physics the forces between them are described by quantum field theories, all of the non-abelian gauge theory type. The electro-weak force is mediated by four exchange particles. These are the mass-less photon (gamma) and the three field particles W+, W – and Z0. The strong force is conveyed by eight mass-less gluons g. Apart from these twelve exchange particles, the theory predicts a very heavy particle, the Higgs particle H0. The field of the Higgs particle generates all particle masses. |
New name for an old theory
Modern theories used today in the standard model of particle physics for describing the interactions of particles are all gauge theories. The term gauge relates to a particular feature of these theories, gauge symmetry, viewed by many researchers as one of the most fundamental features of physics. Yet as early as in the 1860s the Scotsman James Clerk Maxwell formulated a theory of electromagnetism which in today’s modern terminology is a gauge theory. His theory, which still holds, united electricity with magnetism and predicted, among other things, the existence of radio waves.
We can illustrate the concept of gauge symmetry as follows. Electric and magnetic fields can be expressed using potential functions. These can be exchanged (gauge-transformed ) according to a certain rule without changing the fields. The very simplest transformation is to add a constant to the electrical potential. Physically this illustrates the well-known fact that electrical potential can be calculated from an arbitrary zero point, since only the differences in potential are of significance. This is why a squirrel can walk along a high-voltage cable without being injured. That the zero point can be moved in this way is perceived by physicists as a symmetry in the theory, gauge symmetry.
The order in which one performs two gauge transformations is immaterial. We normally say that electromagnetism is an abelian gauge theory, after the Norwegian mathematician Niels Henrik Abel, who lived between 1802 and 1829. (A simple example of transformations that are abelian are plane rotations. Try this yourself with a pencil, as shown in Figure 2a.)
Figure 2a) An example of a group of abelian transformations is rotation in two dimensions.

|
Put a pencil on a table. |
Turn it first 90o |
and then 180o in the same direction. |

|
Do it once again, but now reverse the order: |
Turn it first 180o |
and then 90o. The result is the same! |
Figure 2b) An example of a group of non-abelian transformations is rotation in three-dimensional space.

|
Hold a pencil horizontally with the point to the right. |
Turn it through 90o so that the point points to the floor. |
Then turn it through 180o so that the point points upwards. |

|
Do it once again, but now reverse the order: |
Do the 180° turn first (which does not alter the direction of the point but causes the pencil to turn half a revolution). |
Then do the 90° degree turn (which causes the point to point to the floor). The result is now quite different! |
Quantum mechanics raises problems
Directly after quantum mechanics had been formulated around 1925 attempts were made to unify the wave functions of quantum mechanics and the fields of electromagnetism into a quantum field theory. But problems arose. The new quantum electrodynamics became complicated and attempts to perform calculations often gave unreasonable results. One reason was that quantum theory predicts that the electromagnetic fields close to e.g. an electron or a proton can spontaneously generate quantities of very short-lived particles and anti-particles, virtual particles (Fig. 3). A system of only one electron suddenly became a multi-particle problem!
The problem was solved in the 1940s by Sin-Itiro Tomonaga, Julian Schwinger and Richard P. Feynman (who shared the 1965 Nobel Prize in physics for their contributions). The method developed by these three is called renormalization and, simply expressed, means that individual particles can be viewed “somewhat at a distance”. In this way it is unnecessary to consider the virtual particle pairs individually: the “cloud” of virtual particles can be allowed to obscure the central, original particle. In this way, the original particle gains a new charge and a new mass, among other things. In modern terminology, Tomonaga, Schwinger and Feynman renormalized an abelian gauge theory.

Fig. 3 According to quantum field theory a real “physical” particle consists of a “naked” central particle “dressed” in a cloud of very short-lived so called “virtual” particles.
Quantum electrodynamics has been tested with greater accuracy than any other theory in physics. Thus for example Hans Dehmelt (Nobel Prize in Physics 1989) succeeded in measuring electron magnetism in an ion trap with an accuracy of 12 digits. The first 10 digits agreed directly with calculated results.
Unified electromagnetic and weak interaction
The discovery and study of radioactivity and the subsequent development of atomic physics during the first half of the twentieth century produced the concepts of strong and weak interaction. In simple terms strong interaction holds the atomic nucleus together while weak interaction allows certain nuclei to decay radioactively. As early as the 1930s a first quantum field theory for weak interaction was formulated. This theory suffered from problems that were even worse than those quantum electrodynamics had had and not even the renormalization method of Tomonaga, Schwinger and Feynman could solve them.
But in the mid-1950s the researchers Chen Ning Yang and Robert L. Mills found a first example of a quantum field theory with new features, a non-abelian gauge theory. As opposed to the abelian variant, in which gauge transformations can be performed in any order, the result of the non-abelian depends on the order. This gives the theory a more complicated mathematical structure but also opens up new possibilities. (A simple example of non-abelian transformations is rotations in space. Try it yourself with a pencil, as shown in Figure 2b.)
The new possibilities of the theory were not fully exploited until the 1960s when a number of researchers collaborated in the development of a non-abelian gauge theory that unites electromagnetism and weak interaction into an electro-weak interaction (Nobel Prize 1979 to Sheldon L. Glashow, Abdus Salam and Steven Weinberg). This quantum field theory predicted the new particles W and Z which were detected in 1983 at the European CERN accelerator laboratory in Geneva (Nobel Prize 1984 to Carlo Rubbia and Simon van der Meer).
History repeats itself
While the theory of electro-weak interaction developed in the 1960s was a great step forward, the research community at first found it difficult to accept. When they tried to use the theory for calculating in more detail the properties of the new W and Z particles (and many other physical quantities) it gave unreasonable results. The situation resembled that of the 1930s before Tomonaga, Schwinger and Feynman had succeeded in renormalizing quantum electrodynamics. Many researchers were pessimistic about the possibilities of going further with such a theory.
One person who had not given up hope of being able to renormalize non-abelian gauge theories was Martinus J. G. Veltman. At the end of the 1960s he was a newly appointed professor at the University of Utrecht. Veltman had developed the Schoonschip computer program which, using symbols, performed algebraic simplifications of the complicated expressions that all quantum field theories result in when quantitative calculations are performed. Twenty years earlier, Feynman had indeed systematised the problem of calculation and introduced Feynman diagrams that were rapidly accepted by researchers. But at that time there were no computers. Veltman believed firmly in the possibility of finding a way of renormalizing the theory and his computer program was the cornerstone of the comprehensive work of testing different ideas.
In spring 1969 Veltman was joined by a 22-year-old pupil, Gerardus ‘t Hooft, who had expressed the desire to study high-energy physics. After he had written a first, fairly brief dissertation ‘t Hooft was accepted as a doctoral student that autumn. His task was to help in the search for a method of renormalizing non-abelian gauge theories. ‘t Hooft succeeded beyond all expectation and in 1971 published two articles that represented an important breakthrough in the research programme.
With the help of Veltman’s computer program ‘t Hooft’s partial results were now verified and together they worked out a calculation method in detail. The non-abelian gauge theory of electro-weak interaction had become a functioning theoretic machinery and it was possible, just as it had become for quantum electrodynamics 20 years previously, to start performing precise calculations.
The theory’s predictions verified
As described above, the theory of the electro-weak force predicted the existence of the new W and Z particles right from the start. But it was only through ‘t Hooft’s and Veltman’s work that more precise prediction of physical quantities involving properties of W and Z could start. Large quantities of W and Z have recently been produced under controlled conditions at the LEP accelerator at CERN. Comparisons between measurements and calculations have all the time showed great agreement, thus supporting the theory’s predictions.
One particular quantity obtained with ‘t Hooft’s and Veltman’s calculation method based on CERN results is the mass of the top quark, the heavier of the two quarks included in the third family in the model. This quark was observed directly for the first time in 1995 at the Fermilab in the USA, but its mass had been predicted several years earlier. Here too, agreement between experiment and theory was satisfactory.
When can we expect the next great discovery?
An important ingredient in the theory ‘t Hooft and Veltman have developed is an as yet undemonstrated particle termed the Higgs particle (Fig. 1). In the same way as other particles have been predicted by theoretical arguments and later demonstrated experimentally, researchers are now awaiting direct observation of the Higgs particle. Using calculations similar to those of the mass of the top quark, there is a chance that one of the existing accelerators can be persuaded to produce some Higgs particles. But the only accelerator now under construction and powerful enough for more detailed study of the new particle is the Large Hadron Collider (LHC) at CERN. But researchers must contain themselves for a few years to come since it is reckoned that the LHC will not be complete until 2005.
| Further reading |
| Additional background material on the Nobel Prizes in Physics 1999, by Professor Cecilia Jarlskog, the Royal Swedish Academy of Sciences (pdf). |
| In search of the Ultimate Building Blocks by Gerard ‘t Hooft, Cambridge University Press 1997. |
| The Higgs boson by Martinus J.G. Veltman, Scientific American, November 1986, p.88. |
| An Elementary Primer for Gauge Theory by K. Moriyasu, World Scientific Publishing 1983. |
| Gauge Theories of the Forces between Elementary Particles by Gerard ‘t Hooft, Scientific American, June 1980, p. 90. |
Gerardus ‘t Hooft
born 1946 in Den Helder, the Netherlands. Dutch citizen. Doctoral degree in physics 1972 at University of Utrecht. Professor of Physics at University of Utrecht since 1977. Among other awards ‘t Hooft received the 1979 Dannie Heineman Prize from the American Physical Society and the 1982 Wolf Prize for his work on renormalizing gauge theories. Member of the Dutch Academy of Sciences since 1982.
Professor Gerardus ‘t Hooft
Spinoza Instituut
Leuvenlaan 4
Postbus 80.195
3508 TD Utrecht
The Netherlands
Martinus J. G. Veltman
born 1931 in the Netherlands. Dutch citizen. Doctoral degree in physics 1963 at University of Utrecht. Professor of Physics at University of Utrecht 1966-1981 and at University of Michigan, Ann Arbor, from 1981 (now retired). Among other awards Veltman received the 1993 High Energy and Particle Physics Prize from the European Physical Society for his work on renormalizing gauge theories. Member of the Dutch Academy of Sciences since 1981.
Professor Martinus J. G. Veltman
Schubertlaan 15
3723 LM Bilthoven
The Netherlands
The amount of the Nobel Prize Award is SEK 7,900,000.
Martinus J.G. Veltman – Other resources
Links to other sites
“Hiding Infinites”, Lecture by Martinus Veltman (video) at CERN from Web Lecture Archive Project
On Martinus J.G. Veltman from the Lindau Mediatheque
Science Video Interview from Vega Science Trust
Gerardus ‘t Hooft – Photo gallery
Gerardus 't Hooft receiving his Nobel Prize from His Majesty King Carl XVI Gustaf of Sweden at the Stockholm Concert Hall,
10 December 1999.
Copyright © The Nobel Foundation 1999
Photo: Hans Mehlin
Gerardus 't Hooft after receiving his Nobel Prize from His Majesty the King.
Copyright © The Nobel Foundation 1999
Photo: Hans Mehlin
All 1999 Nobel Laureates onstage. Martinus J.G. Veltman is second from left.
Copyright © The Nobel Foundation 1999
Photo: Hans Mehlin
© The Nobel Foundation 1999. Photo: Hans Mehlin
The Nobel Prize Award Ceremony at the Stockholm Concert
Hall. From left, Laureates Gerardus 't Hooft, Martinus J.G. Veltman
and Ahmed Zewail.
Copyright © The Nobel Foundation 1999
Photo: Hans Mehlin
Martinus J.G. Veltman – Photo gallery
Martinus J.G. Veltman receiving his Nobel Prize from His Majesty King Carl XVI Gustaf of Sweden at the Stockholm Concert Hall, 10 December 1999. Copyright © The Nobel Foundation 1999
Photo: Hans Mehlin
Martinus J.G. Veltman receiving his Nobel Prize from His Majesty King Carl XVI Gustaf of Sweden at the Stockholm Concert Hall, 10 December 1999. [snippet id="11708"]
Martinus J.G. Veltman after receiving his Nobel Prize from His Majesty the King. Copyright © The Nobel Foundation 1999
Photo: Hans Mehlin
Martinus J.G. Veltman after receiving his Nobel Prize from His Majesty the King. [snippet id="11708"]
All 1999 Nobel Laureates onstage. Martinus J.G. Veltman is second from left.
Copyright © The Nobel Foundation 1999
Photo: Hans Mehlin
© The Nobel Foundation 1999. Photo: Hans Mehlin
The Nobel Prize Award Ceremony at the Stockholm Concert
Hall. From left, Laureates Gerardus 't Hooft, Martinus J.G. Veltman
and Ahmed Zewail.
Copyright © The Nobel Foundation 1999
Photo: Hans Mehlin
Queen Silvia of Sweden and Nobel Laureate Martinus J.G. Veltman at the Nobel Banquet.
© Pressens Bild AB 1999, S-112 88 Stockholm, Sweden, telephone: +46(0)87383800. Photo: Jonas Ekströmer
Martinus J.G. Veltman – Nobel diploma

Copyright © The Nobel Foundation 1999
Artist: Nils G Stenqvist
Calligrapher: Annika Rücker
Gerardus ‘t Hooft – Other resources
Links to other sites
Home page of Professor Gerardus ‘t Hooft at Utrecht University