Press release
English
German
French
Swedish

12 October 1999
The Royal Swedish Academy of Sciences has awarded the 1999 Nobel Prize in Physics jointly to
Professor Gerardus ‘t Hooft, University of Utrecht, Utrecht, the Netherlands, and
Professor Emeritus Martinus J. G. Veltman, University of Michigan, USA, resident in Bilthoven, the Netherlands.
The two researchers are being awarded the Nobel Prize for having placed particle physics theory on a firmer mathematical foundation. They have in particular shown how the theory may be used for precise calculations of physical quantities. Experiments at accelerator laboratories in Europe and the USA have recently confirmed many of the calculated results.
The Academy’s citation:
“for elucidating the quantum structure of electroweak interactions in physics”
Particle physics theory on firmer mathematical foundation
The everyday objects in our surroundings are all built up of atoms, which consist of electrons and atomic nuclei. In the nuclei there are protons and neutrons, which in turn are made up of quarks. To study matter at this innermost level, large accelerators are required. Such machines were first designed in the 1950s, signifying the birth of modern particle physics. For the first time it was possible to study the creation of new particles and the forces that act between them.
Around the middle of the 1950s, a first version of the modern theory was also formulated. Many years of work have now resulted in the standard model of particle physics. This model groups all elementary particles into three families of quarks and leptons, which interact with the help of a number of exchange particles for the strong and the electro-weak forces (Fig 1).
The theoretical foundation of the standard model was at first incomplete mathematically and in particular it was unclear whether the theory could be used at all for detailed calculations of physical quantities. Gerardus ‘t Hooft and Martinus J. G. Veltman are being awarded this year’s Nobel Prize for having placed this theory on a firmer mathematical foundation. Their work has given researchers a well functioning “theoretical machinery” which can be used for, among other things, predicting the properties of new particles.
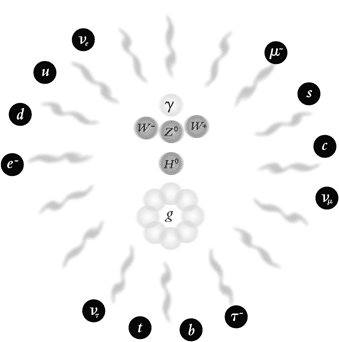 |
| Fig. 1. Matter’s fundamental particles are six leptons and six quarks. In the standard model of particle physics the forces between them are described by quantum field theories, all of the non-abelian gauge theory type. The electro-weak force is mediated by four exchange particles. These are the mass-less photon (gamma) and the three field particles W+, W – and Z0. The strong force is conveyed by eight mass-less gluons g. Apart from these twelve exchange particles, the theory predicts a very heavy particle, the Higgs particle H0. The field of the Higgs particle generates all particle masses. |
New name for an old theory
Modern theories used today in the standard model of particle physics for describing the interactions of particles are all gauge theories. The term gauge relates to a particular feature of these theories, gauge symmetry, viewed by many researchers as one of the most fundamental features of physics. Yet as early as in the 1860s the Scotsman James Clerk Maxwell formulated a theory of electromagnetism which in today’s modern terminology is a gauge theory. His theory, which still holds, united electricity with magnetism and predicted, among other things, the existence of radio waves.
We can illustrate the concept of gauge symmetry as follows. Electric and magnetic fields can be expressed using potential functions. These can be exchanged (gauge-transformed ) according to a certain rule without changing the fields. The very simplest transformation is to add a constant to the electrical potential. Physically this illustrates the well-known fact that electrical potential can be calculated from an arbitrary zero point, since only the differences in potential are of significance. This is why a squirrel can walk along a high-voltage cable without being injured. That the zero point can be moved in this way is perceived by physicists as a symmetry in the theory, gauge symmetry.
The order in which one performs two gauge transformations is immaterial. We normally say that electromagnetism is an abelian gauge theory, after the Norwegian mathematician Niels Henrik Abel, who lived between 1802 and 1829. (A simple example of transformations that are abelian are plane rotations. Try this yourself with a pencil, as shown in Figure 2a.)
Figure 2a) An example of a group of abelian transformations is rotation in two dimensions.
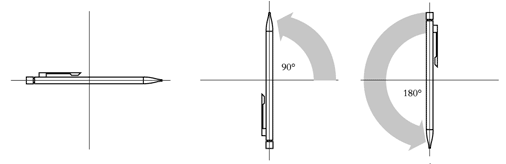
|
Put a pencil on a table. |
Turn it first 90o |
and then 180o in the same direction. |
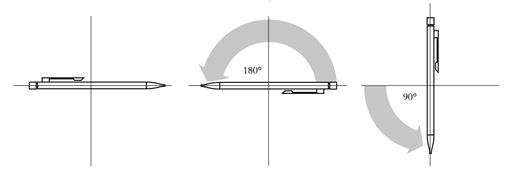
|
Do it once again, but now reverse the order: |
Turn it first 180o |
and then 90o. The result is the same! |
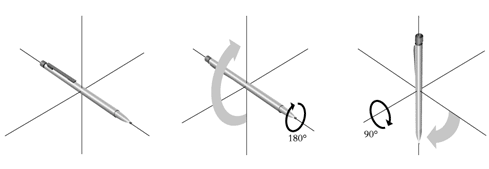
Figure 2b) An example of a group of non-abelian transformations is rotation in three-dimensional space.
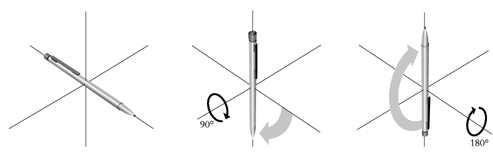
|
Hold a pencil horizontally with the point to the right. |
Turn it through 90o so that the point points to the floor. |
Then turn it through 180o so that the point points upwards. |
|
Do it once again, but now reverse the order: |
Do the 180° turn first (which does not alter the direction of the point but causes the pencil to turn half a revolution). |
Then do the 90° degree turn (which causes the point to point to the floor). The result is now quite different! |
Quantum mechanics raises problems
Directly after quantum mechanics had been formulated around 1925 attempts were made to unify the wave functions of quantum mechanics and the fields of electromagnetism into a quantum field theory. But problems arose. The new quantum electrodynamics became complicated and attempts to perform calculations often gave unreasonable results. One reason was that quantum theory predicts that the electromagnetic fields close to e.g. an electron or a proton can spontaneously generate quantities of very short-lived particles and anti-particles, virtual particles (Fig. 3). A system of only one electron suddenly became a multi-particle problem!
The problem was solved in the 1940s by Sin-Itiro Tomonaga, Julian Schwinger and Richard P. Feynman (who shared the 1965 Nobel Prize in physics for their contributions). The method developed by these three is called renormalization and, simply expressed, means that individual particles can be viewed “somewhat at a distance”. In this way it is unnecessary to consider the virtual particle pairs individually: the “cloud” of virtual particles can be allowed to obscure the central, original particle. In this way, the original particle gains a new charge and a new mass, among other things. In modern terminology, Tomonaga, Schwinger and Feynman renormalized an abelian gauge theory.
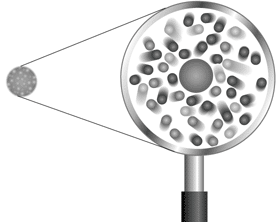
Fig. 3 According to quantum field theory a real “physical” particle consists of a “naked” central particle “dressed” in a cloud of very short-lived so called “virtual” particles.
Quantum electrodynamics has been tested with greater accuracy than any other theory in physics. Thus for example Hans Dehmelt (Nobel Prize in Physics 1989) succeeded in measuring electron magnetism in an ion trap with an accuracy of 12 digits. The first 10 digits agreed directly with calculated results.
Unified electromagnetic and weak interaction
The discovery and study of radioactivity and the subsequent development of atomic physics during the first half of the twentieth century produced the concepts of strong and weak interaction. In simple terms strong interaction holds the atomic nucleus together while weak interaction allows certain nuclei to decay radioactively. As early as the 1930s a first quantum field theory for weak interaction was formulated. This theory suffered from problems that were even worse than those quantum electrodynamics had had and not even the renormalization method of Tomonaga, Schwinger and Feynman could solve them.
But in the mid-1950s the researchers Chen Ning Yang and Robert L. Mills found a first example of a quantum field theory with new features, a non-abelian gauge theory. As opposed to the abelian variant, in which gauge transformations can be performed in any order, the result of the non-abelian depends on the order. This gives the theory a more complicated mathematical structure but also opens up new possibilities. (A simple example of non-abelian transformations is rotations in space. Try it yourself with a pencil, as shown in Figure 2b.)
The new possibilities of the theory were not fully exploited until the 1960s when a number of researchers collaborated in the development of a non-abelian gauge theory that unites electromagnetism and weak interaction into an electro-weak interaction (Nobel Prize 1979 to Sheldon L. Glashow, Abdus Salam and Steven Weinberg). This quantum field theory predicted the new particles W and Z which were detected in 1983 at the European CERN accelerator laboratory in Geneva (Nobel Prize 1984 to Carlo Rubbia and Simon van der Meer).
History repeats itself
While the theory of electro-weak interaction developed in the 1960s was a great step forward, the research community at first found it difficult to accept. When they tried to use the theory for calculating in more detail the properties of the new W and Z particles (and many other physical quantities) it gave unreasonable results. The situation resembled that of the 1930s before Tomonaga, Schwinger and Feynman had succeeded in renormalizing quantum electrodynamics. Many researchers were pessimistic about the possibilities of going further with such a theory.
One person who had not given up hope of being able to renormalize non-abelian gauge theories was Martinus J. G. Veltman. At the end of the 1960s he was a newly appointed professor at the University of Utrecht. Veltman had developed the Schoonschip computer program which, using symbols, performed algebraic simplifications of the complicated expressions that all quantum field theories result in when quantitative calculations are performed. Twenty years earlier, Feynman had indeed systematised the problem of calculation and introduced Feynman diagrams that were rapidly accepted by researchers. But at that time there were no computers. Veltman believed firmly in the possibility of finding a way of renormalizing the theory and his computer program was the cornerstone of the comprehensive work of testing different ideas.
In spring 1969 Veltman was joined by a 22-year-old pupil, Gerardus ‘t Hooft, who had expressed the desire to study high-energy physics. After he had written a first, fairly brief dissertation ‘t Hooft was accepted as a doctoral student that autumn. His task was to help in the search for a method of renormalizing non-abelian gauge theories. ‘t Hooft succeeded beyond all expectation and in 1971 published two articles that represented an important breakthrough in the research programme.
With the help of Veltman’s computer program ‘t Hooft’s partial results were now verified and together they worked out a calculation method in detail. The non-abelian gauge theory of electro-weak interaction had become a functioning theoretic machinery and it was possible, just as it had become for quantum electrodynamics 20 years previously, to start performing precise calculations.
The theory’s predictions verified
As described above, the theory of the electro-weak force predicted the existence of the new W and Z particles right from the start. But it was only through ‘t Hooft’s and Veltman’s work that more precise prediction of physical quantities involving properties of W and Z could start. Large quantities of W and Z have recently been produced under controlled conditions at the LEP accelerator at CERN. Comparisons between measurements and calculations have all the time showed great agreement, thus supporting the theory’s predictions.
One particular quantity obtained with ‘t Hooft’s and Veltman’s calculation method based on CERN results is the mass of the top quark, the heavier of the two quarks included in the third family in the model. This quark was observed directly for the first time in 1995 at the Fermilab in the USA, but its mass had been predicted several years earlier. Here too, agreement between experiment and theory was satisfactory.
When can we expect the next great discovery?
An important ingredient in the theory ‘t Hooft and Veltman have developed is an as yet undemonstrated particle termed the Higgs particle (Fig. 1). In the same way as other particles have been predicted by theoretical arguments and later demonstrated experimentally, researchers are now awaiting direct observation of the Higgs particle. Using calculations similar to those of the mass of the top quark, there is a chance that one of the existing accelerators can be persuaded to produce some Higgs particles. But the only accelerator now under construction and powerful enough for more detailed study of the new particle is the Large Hadron Collider (LHC) at CERN. But researchers must contain themselves for a few years to come since it is reckoned that the LHC will not be complete until 2005.
| Further reading |
| Additional background material on the Nobel Prizes in Physics 1999, by Professor Cecilia Jarlskog, the Royal Swedish Academy of Sciences (pdf). |
| In search of the Ultimate Building Blocks by Gerard ‘t Hooft, Cambridge University Press 1997. |
| The Higgs boson by Martinus J.G. Veltman, Scientific American, November 1986, p.88. |
| An Elementary Primer for Gauge Theory by K. Moriyasu, World Scientific Publishing 1983. |
| Gauge Theories of the Forces between Elementary Particles by Gerard ‘t Hooft, Scientific American, June 1980, p. 90. |
Gerardus ‘t Hooft
born 1946 in Den Helder, the Netherlands. Dutch citizen. Doctoral degree in physics 1972 at University of Utrecht. Professor of Physics at University of Utrecht since 1977. Among other awards ‘t Hooft received the 1979 Dannie Heineman Prize from the American Physical Society and the 1982 Wolf Prize for his work on renormalizing gauge theories. Member of the Dutch Academy of Sciences since 1982.
Professor Gerardus ‘t Hooft
Spinoza Instituut
Leuvenlaan 4
Postbus 80.195
3508 TD Utrecht
The Netherlands
Martinus J. G. Veltman
born 1931 in the Netherlands. Dutch citizen. Doctoral degree in physics 1963 at University of Utrecht. Professor of Physics at University of Utrecht 1966-1981 and at University of Michigan, Ann Arbor, from 1981 (now retired). Among other awards Veltman received the 1993 High Energy and Particle Physics Prize from the European Physical Society for his work on renormalizing gauge theories. Member of the Dutch Academy of Sciences since 1981.
Professor Martinus J. G. Veltman
Schubertlaan 15
3723 LM Bilthoven
The Netherlands
The amount of the Nobel Prize Award is SEK 7,900,000.
Nobel Prizes and laureates
See them all presented here.
