Advanced information

Additional background material on the Nobel Prize in Physics 1996
The Royal Swedish Academy of Sciences has decided to award the 1996 Nobel Prize in Physics jointly to
Professor David M. Lee, Cornell University, Ithaca, NY, USA,
Professor Douglas D. Osheroff, Stanford University, Stanford, CA, USA, and
Professor Robert C. Richardson, Cornell University, Ithaca, NY, USA,
for their discovery of superfluidity in helium-3.
This additional background material gives a short account of the discovery and its importance and is written mainly for physicists.
1. A breakthrough in low temperature physics
The pioneering work of David Lee, Douglas Osheroff and Robert Richardson in the beginning of the 1970’s at the low-temperature laboratory of Cornell University has given a most valuable contribution to our current view of the manifestations of quantum effects in bulk matter. The anisotropic superfluid helium-3, appearing below a critical temperature of about two thousandths of a degree above the absolute zero, is considered to be a particular kind of Bose-Einstein condensate with a rich set of physical properties. The study of this exotic quantum liquid has led to concepts that are of general importance and, e.g., could become useful for the theoretical treatment of high temperature superconductors. Recently phase transitions in helium-3 have been studied as a model for the dynamics of the cosmological phase transitions that are thought to have occurred a fraction of a second after the Big Bang (see Nature, July 25, and Science, August 2, 1996). Critical points of superfluid helium-3 are used to define temperature scales at values extremely close to the absolute zero.
2. The discovery
Superfluidity in helium-3 first manifested itself as small anomalies in the melting curve of solid helium-3, i.e. as small structures in the diagram representing pressure against time, when the fluid was cooled. It is always tempting to consider small deviations as more or less inexplicable peculiarities of the equipment, but the discoverers became convinced that there was a real effect. They were actually not looking for superfluidity, but for an antiferromagnetic phase in solid helium-3, which according to predictions was to appear below 2 mK. It was thus natural that they, in their first publication 1972, interpreted the effect as the observation of such a phase transition.
The agreement was not perfect, but by further development of their technique and new measurements they could, just a few months later, pinpoint the effect. It actually turned out to involve two phase transitions in the liquid phase, at 2.7 and 1.8 mK respectively.
The discovery became the starting point of an intense activity among low temperature physicists. The experimental and theoretical developments went hand-in-hand in an unusally fruitful way. The field was rapidly mapped out, but fundamental discoveries are still being made.
3. Particle statistics and superfluidity
In quantum physics the atoms in a gas are described by a wavefunction which is a function of all the coordinates of the atoms, but which only specifies the probability of finding a particle in a given region at a given time. In the quantum regime (which applies at high density or low temperature) the indistinguishability of the atoms leads to dramatic quantum effects. In nature there are two fundamental types of particles, fermions and bosons. Fermions have half-integral spin and are described by wavefunctions that are antisymmetric in the exchange of two particles, i.e. the wavefunctions change sign when two particles change places, and they follow what is called Fermi-Dirac statistics. Bosons have integral spin and symmetric wavefunctions, i.e. their wavefunctions are unchanged when two particles are exchanged, and they follow Bose-Einstein statistics. Fermions tend to avoid each other and a gas of fermions can have at most one particle in each one-particle quantum state. Bosons, on the other hand, are more sociable and can occupy the same quantum state. Below a certain temperature, which depends on the particle density, the bosons tend to gather in a Bose-Einstein condensate in the quantum state of the lowest energy and momentum. They are then described by one and the same wavefunction.
A pure Bose-Einstein condensate of (bosonic) atoms that only interact weakly was not experimentally produced until last year. Then a number of groups managed to cool small samples of dilute gases to temperatures well below one microkelvin. But a type of Bose-Einstein condensate, with atoms condensed into the ground state, was identified already in the 1930’s, namely the superfluid phase of helium. This quantum liquid is freely flowing (without viscosity), can penetrate fine pores that are closed for ordinary liquids and for many gases, can creep upwards along walls and is an excellent heat conductor.
Helium mainly consists of the isotope helium-4, which is a boson (electronic and nuclear spins are zero). The more rare isotope helium-3, on the other hand, has nuclear spin 1/2, is a fermion and as such cannot undergo Bose-Einstein condensation. But in explaining the phenomenon of superconductivity in metals in 1957, Bardeen, Cooper and Schrieffer showed that fermions (in this case electrons) under certain conditions can make up pairs (Cooper pairs) that behave as bosons. These pairs can then undergo condensation to a ground state. In principle this explains the 1972 finding of the phenomenon of superfluidity in helium-3 by Lee, Osheroff and Richardson. But the nature of the pairing and the properties of the pairs are very different in the two cases.
In a superconducting metal it is the surrounding lattice of positive ions that provides the mechanism making it possible to pair together electrons with opposite momenta and spin to quasiparticles having zero orbital angular momentum or spin (L=S=0). In the superfluid phase of helium-3 the atoms themselves provide the pairing interaction, through magnetic interaction (the superfluid phase is almost ferromagnetic), and the pairs are more complicated. The atoms in the pair rotate around each other and the pair has one unit of internal orbital angular momentum (L=1). The nuclear spin magnetic moments tend to be oriented along a common direction (S=1). The wave function which describes the pair is a complex valued function and has both amplitude and phase. This means that the wavefunction of a superfluid helium-3 pair has 2(2L+1)(2S+1)=18 real components, as compared to 2 for the superconducting electron pair. Even though some components are coupled to each other (there is a spontaneous breaking of the symmetry in spin-orbit space) the wave function is still quite complicated and gives rise to a rich set of orientational effects.
In the condensate, the bosonic quasiparticle pairs are coupled to each other and can be described by a macroscopic wave function with a well defined phase. This means that the pairs, with their spinning nuclei and partners rotating around each other, all move coherently so that their individual nuclear spins and orbital angular momenta are coupled to a correlated state with large spatial extension. Some consequences of this are that a minimum energy (gap energy) is needed to break up the condensate, that the liquid cannot rotate freely above a critical rotational velocity, but vortices appear with quantized circulation, and that Josephson effects appear, e.g., leading to a kind of “ringing” in the liquid after the variation of a magnetic field over the sample. Most of the theoretical concepts regarding the paired state and the pairing mechanism were developed already before the experimental discovery, by, among others, Anderson and Morel (later on also with Brinkman), by Vdovin, and by Balian and Werthamer, and others. Experiments on superfluid helium-3 have later on helped to discriminate among different theories.
4. The experimental technique
Helium is an inert gas that is present as a small component in ordinary air (about one part in 200 000). But the fraction of the isotope helium-3 is about one million times smaller and it would be too costly to extract it out of air or out of ordinary helium gas. Instead it can be produced by irradiation of lithium by neutrons from a nuclear reactor. After the nuclear reaction and beta decay a gas rich in helium-3 is left, which is sold at a high price.
Both isotopes of He are inert and light gases, which among other things means that their electronic dipole polarizabilities are small, thus making the van der Waals interaction between individual atoms weak, but also that the zero point motion is large. This implies that the condensed gas, liquid helium, does not freeze at ordinary pressure, but remains in liquid form even at temperatures close to the absolute zero. In this respect helium is unique among all the elements of the periodic table. It is only under high pressure at low temperatures that the liquid helium crystallizes and transforms into a solid phase.
Several powerful techniques for cooling were developed during the 1960’s. Lee, Osheroff and Richardson used a method that had been proposed by Pomeranchuk and which was put into practical use by Anufriev and later developed by, among others, the scientists at Cornell. The method makes use of the remarkable property of helium-3 that the liquid phase at low temperature is more well-ordered than the solid phase. (Ordinary liquids are much more disordered, have a higher entropy, than the corresponding crystals, with their periodically ordered rows of atoms.) By applying a pressure to the liquid, some parts of it are transformed into the solid phase. These parts thus transform from a higher to a lower order, for which heat is needed (cf. the melting of an ordinary crystal). This heat is taken from the remaining liquid, which thus is cooled further.
Using Pomeranchuk cooling one can reach a final temperature just below 2 mK before all the liquid has been transformed into the solid phase. The process is hampered by not being continuous, but it has several positive properties. The cooling power is high and the heat contact with the liquid helium-3 sample is good, since the cooling medium is the same as the sample. At very low temperatures it can otherwise be difficult to get a good heat contact; it can easily happen that the cooling agent, the sample and the thermometer have different temperatures. Different excitations (e.g., thermal motions among the atoms, spin waves and electrons) may also not be in thermal equilibrium.
5. Discovery and properties of superfluid helium-3
The scientists at Cornell were low temperature specialists and had built their own apparatus. But in their first measurements on helium-3 they had a problem with their thermometer at below a few thousandths of a degree from absolute zero. They decided to monitor the internal pressure in the sample under an external pressure that increased uniformly with time. It was the research student Osheroff who observed a change in the way the internal pressure varied with time. He did not put the observation aside as being due to some feature of the apparatus, but instead insisted that it was a real effect. He observed two anomalies, shown in Fig. 1. They turned out to be the transition to phase A, where the individual members of the boson pairs have parallel spins, and to the phase B, in which they have both parallel and anti-parallel spins. (In a magnetic field, phase A will increase at the expense of phase B, as seen in a pressure-against-temperature diagram. Then also a new phase (A1) appears, in which the pairs have atoms with parallel spins (as in phase A) and they all point in the same direction.)
Another speciality of the group at Cornell was the nuclear magnetic resonance technique (NMR). In an applied magnetic field the nuclear spins of the sample atoms will rotate around the field lines. The frequency of rotation is given by the strength of the field and by the magnetic moments of the nuclei. When the frequency becomes equal to that of an applied radio frequency (r.f.) field, resonance appears and the absorption of the r.f. field increases. This kind of measurement gives valuable information on the magnetic state of the helium-3 nuclei. Lee, Osheroff and Richardson found characteristic changes of the resonance frequency at the phase transition, changes that are dependent on the magnetic field strength and on the temperature and are different in the A and B phases. The theoretician Leggett could, within a few weeks, explain the characteristic behaviour in detail. He showed that in each pair the nuclear spins are coupled with the rotation, and pointed out the importance of the phase of the macroscopic wave function that describes the condensate.
The fact that the new phases of helium-3 really were superfluid and could flow without resistance was shown by two groups soon after the discovery. A group at the University of Technology in Helsinki, led by Olli Lounasmaa, measured the damping of a string vibrating in the liquid. They showed that the damping diminished by a factor of about 1 000 as the liquid was cooled from above 2 mK to 1 mK. The group led by the late John Wheatley at La Jolla detected and measured the velocity of the so-called fourth order sound. This is not a pressure or density wave, as in ordinary sound, but a temperature wave at constant pressure appearing in fine pores. A persistent flow experiment in Helsinki showed that the flow of superfluid helium-3 in a torus, with packed powder and helium-3 inside, did not decay, at least on the scale of a few days, in the B phase (but not in the anisotropic A phase). This implied a viscosity at least 12 orders of magnitude smaller than the one in the normal fluid helium-3.
6. Research on superfluid helium-3 today
The most convincing experiments testing the coherence of a superfluid are probably those showing the appearance of quantized vortices. When a superfluid is set in rotation and the velocity of rotation exceeds a critical value, microscopic vortices appear. The circulation around such a vortex cannot take on any arbitrary value, but is quantized. This is known from “ordinary” superfluid helium. In helium-3 the vortices can take on complicated appearances, in fact eight different types of vortices have been seen with discontinuous or continuous flow in the vortex cores. Each of them represents a novel topological object with peculiar symmetry and structure. NMR, vibrating strings and other methods have been applied to study the detailed structure of vortices. Their appearance can even be observed directly, through an optical fibre and a cooled CCD camera, as done by the Finnish group which looked on the surface of a rotating sample.
Another topical field of study is textures, similar to those appearing in liquid crystals, with nuclear spins and orbital angular momenta pointing in different directions in different domains of the liquid. The influence of boundary surfaces on the orientation of the liquid, the nucleation and time dependence of phase transitions are also studied.
The phase transitions in helium-3 have recently been used by two different experimental groups (Grenoble and Helsinki) in attempts to simulate the formation of cosmic strings in the early universe. These hypothetical strings might have appeared as topological defects in the rapid phase transitions that are thought to have broken the symmetry of the originally unified interaction and given rise to the four fundamental forces as we know them today (strong, electromagnetic, weak, gravitational). Both groups used neutron induced nuclear reactions to heat their samples locally in such an abrupt way that the well localised phase transitions were accompanied by vortex formation, these vortices being the analogues of the cosmic strings. The validity of a theory formulated by Zurek, following an idea by Kibble, thus seems to have been confirmed. The cosmic strings are believed to be of importance, e.g., for the formation of galaxies.
7. Summary
Superfluidity in helium-3 only appears at very low temperatures, below about 2 mK, and has found practical applications only for specialists in the extreme low temperature techniques. Its main importance has been to develop our understanding of the complicated behaviour of strongly interacting many-particle quantum systems, such as quantum liquids, and for the development of theoretical concepts in the field of macroscopic quantum phenomena. The understanding of high temperature superconductivity, which is still not complete, has gained from concepts developed for helium-3, giving examples of the interactions that lead to pairing of particles in strongly interacting systems as well as for the symmetry of the wave function for such pairs. As a practical application, the polycritical point, where the superfluid phases A and B are in equilibrium with the normal liquid phase, is also used as a fixed point to define temperature scales at very low temperatures.
8. Further reading
“Superfluid Helium 3”, by N.D. Mermin and D.M. Lee, Scientific American, December 1976, p. 56.
“Low temperature science – what remains for the physicist?”, by R.C. Richardson, Physics Today, August 1981, p. 46.
Special Issue: He3 and He4, Physics Today, February 1987, including among other articles “Novel magnetic properties of solid helium-3”, by M.C. Cross and D.D. Osheroff, p. 34.
“The 3He Superfluids”, by O.V. Lounasmaa and G.R. Pickett, Scientific American, June 1990.
“The Superfluid Phases of Helium 3”, by D. Vollhardt and P. Wölfle, Taylor and Francis 1990.
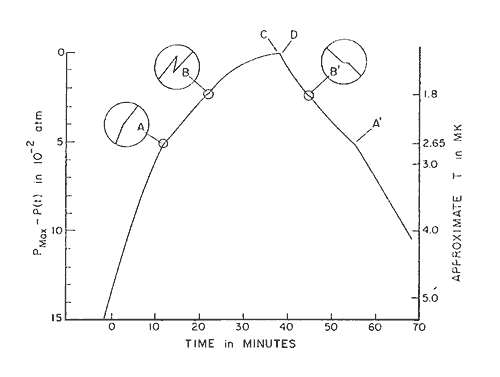
Figure 1. Time dependence of the internal pressure in a Pomeranchuk cell containing a mixture of liquid and solid helium-3 under a cycle of uniform compression and decompression. Note the change in slope of the curves at the points A and B and the temperatures at which they appear. The curve is taken from a paper published by D.D. Osheroff, R.C. Richardson, and D.M. Lee in Physical Review Letters 28, 885 (1972), which gives the first description of the new phase transition in helium-3.
Nobel Prizes and laureates
See them all presented here.
