Popular information
Information for the public:
Crystals of golden proportions (pdf)
Populärvetenskaplig information:
Kristaller av ett gyllene snitt (pdf)

The Nobel Prize in Chemistry 2011
When Dan Shechtman entered the discovery awarded with the Nobel Prize in Chemistry 2011 into his notebook, he jotted down three question marks next to it. The atoms in the crystal in front of him yielded a forbidden symmetry. It was just as impossible as a football – a sphere – made of only sixcornered polygons. Since then, mosaics with intriguing patterns and the golden ratio in mathematics and art have helped scientists to explain Shechtman’s bewildering observation.
Crystals of golden proportions
“Eyn chaya kazo”, Dan Shechtman said to himself. “There can be no such creature” in Hebrew. It was the morning of 8 April 1982. The material he was studying, a mix of aluminium and manganese, was strangelooking, and he had turned to the electron microscope in order to observe it at the atomic level. However, the picture that the microscope produced was counter to all logic: he saw concentric circles, each made of ten bright dots at the same distance from each other (figure 1).
Shechtman had rapidly chilled the glowing molten metal, and the sudden change in temperature should have created complete disorder among the atoms. But the pattern he observed told a completely different story: the atoms were arranged in a manner that was contrary to the laws of nature. Shechtman counted and recounted the dots. Four or six dots in the circles would have been possible, but absolutely not ten. He made a notation in his notebook: 10 Fold???
Crests and troughs in cooperation
In order to understand Shechtman’s experiment and why he was so surprised, imagine the following classroom experiment. A physics teacher transmits light through a perforated metal plate, a so-called diffraction grating (figure 2). When the light waves travel through the grating, they are refracted in the same manner as an ocean wave that moves through a gap in a breakwater.
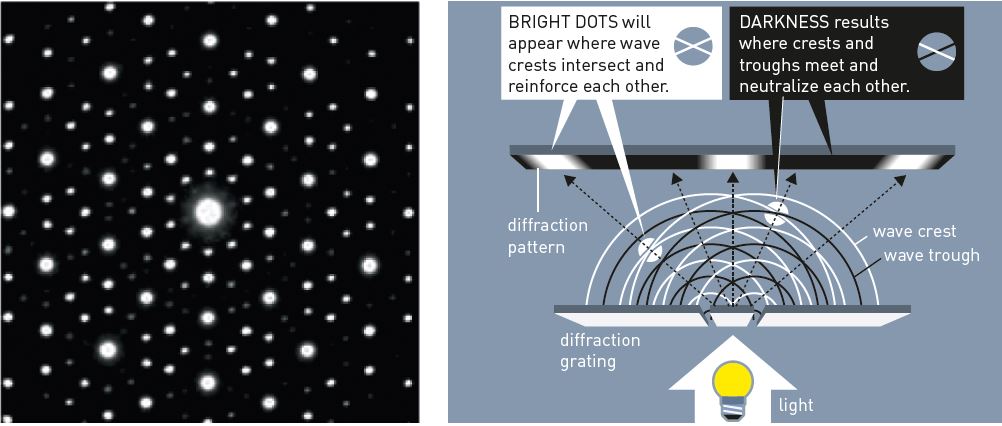
Figure 2. Light passing through a diffraction grating gets scattered. The resulting waves interfere with each other, giving a diffraction pattern. © Johan Jarnestad/The Royal Swedish Academy of Sciences
On the other side of the grating, waves spread in a semicircular manner and intersect with other waves. Crests and troughs of the waves reinforce and counteract each other. On a screen behind the diffraction grating, a pattern will appear of light and dark areas – a diffraction pattern.
It was such a diffraction pattern (figure 1) that Dan Shechtman obtained that April morning in 1982. However, his experiment was different: he used electrons instead of light, his grating consisted of the atoms in the rapidly cooled metal, and he conducted his experiment in three dimensions.
The diffraction pattern showed that the atoms inside the metal were packed into an ordered crystal. That in itself was nothing extraordinary. Almost all solid materials, from ice to gold, consist of ordered crystals. However, the diffraction pattern with ten bright dots arranged in a circle was something he had never seen before, despite his vast experience using electron microscopes. Furthermore, such a crystal was not represented in the International Tables for Crystallography – the main crystallographic reference guide. At the time, science plainly stipulated that a pattern with ten dots in a circle was impossible, and the proof for that was as simple as it was obvious.
A pattern counter to all logic
Inside a crystal, atoms are ordered in repeating patterns, and depending on the chemical composition, they have different symmetries. In figure 3a, we see that each atom is surrounded by three identical atoms in a repeating pattern, yielding a threefold symmetry. Rotate the image 120 degrees and the same pattern will appear.
The same principle applies to fourfold symmetries (figure 3b) and sixfold symmetries (figure 3c). The pattern repeats itself and if you rotate the image, 90 degrees and 60 degrees, respectively, the same pattern appears.
However, with fivefold symmetry (figure 3d), this is not possible, as distances between certain atoms will be shorter than between others. The pattern does not repeat itself, which was proof enough to scientists that it was not possible to obtain fivefold symmetries in crystals. The same applies to sevenfold or higher symmetries.
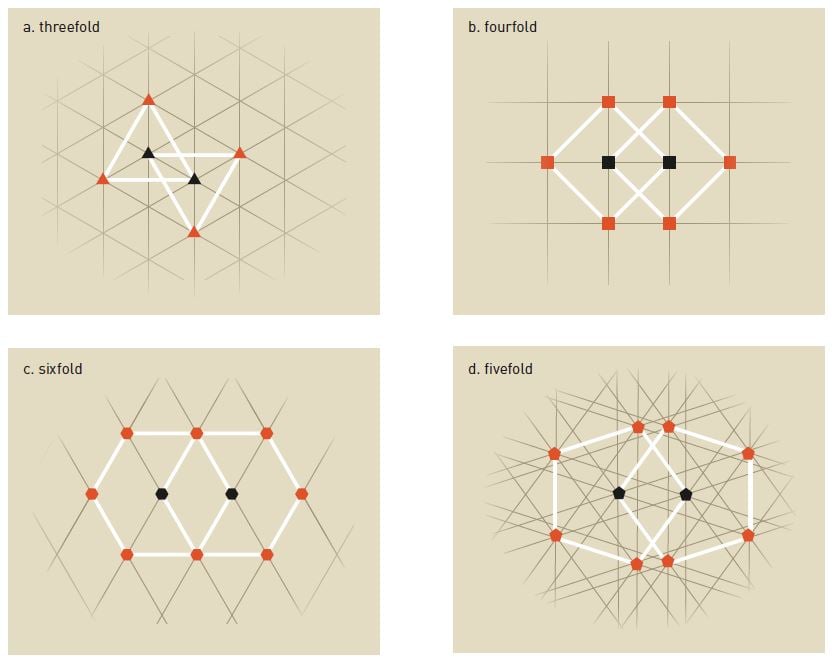
Shechtman, however, could rotate his diffraction pattern by a tenth of a full circle (36 degrees) and still obtain the same pattern. Hence he was looking at a tenfold symmetry, one that was considered impossible. It is no surprise, then, that he made no less than three question marks in his notebook.
Wrong according to the textbook
Dan Shechtman peeked out from his office into the corridor at the U.S. National Institute of Standards and Technology (NIST), wanting to find someone with whom he could share his discovery. But the corridor was empty, so he went back to the microscope to carry out further experiments on the peculiar crystal. Among other things, he double-checked if he had obtained a twin crystal: two intergrown crystals whose shared boundary gives rise to strange diffraction patterns. But he could not detect any signs that he was in fact looking at a twin crystal.
In addition to this, he rotated the crystal in the electron microscope in order to see how far he could turn it before the tenfold diffraction pattern reappeared. That experiment showed that the crystal itself did not have tenfold symmetry like the diffraction pattern, but was instead based on an equally impossible fivefold symmetry. Dan Shechtman concluded that the scientific community must be mistaken in its assumptions.
When Shechtman told scientists about his discovery, he was faced with complete opposition, and some colleagues even resorted to ridicule. Many claimed that what he had observed was in fact a twin crystal. The head of the laboratory gave him a textbook of crystallography and suggested he should read it. Shechtman, of course, already knew what it said but trusted his experiments more than the textbook. All the commotion finally led his boss to ask him to leave the research group, as Schechtman himself recalled later. The situation had become too embarrassing.
Fighting established knowledge
Dan Shechtman had obtained his Ph.D. from Technion – Israel Institute of Technology, and in 1983, he managed to get Ilan Blech, a colleague at his alma mater, interested in his peculiar research findings. Together they attempted to interpret the diffraction pattern and translate it to the atomic pattern of a crystal. They submitted an article to the Journal of Applied Physics in the summer of 1984. But the article came back seemingly by return of post – the editor had refused it immediately.
Shechtman then asked John Cahn, a renowned physicist who had lured him over to NIST in the first place, to take a look at his data. The otherwise busy researcher eventually did, and in turn, Cahn consulted with a French crystallographer, Denis Gratias, in order to see if Shechtman could have missed something. But according to Gratias, Shechtman’s experiments were reliable. Gratias would have proceeded in the same manner had he conducted the experiments himself.
In November 1984, together with Cahn, Blech and Gratias, Shechtman finally got to publish his data in Physical Review Letters. The article went off like a bomb among crystallographers. It questioned the most fundamental truth of their science: that all crystals consist of repeating, periodic patterns.
Removing the blindfold
The discovery now reached a wider audience, and Dan Shechtman became the target of even more criticism. At the same time, however, crystallographers around the world had a moment of déjà vu. Many of them had obtained similar diffraction patterns during analyses of other materials, but had interpreted those patterns as evidence of twin crystals. Now they started digging around in their drawers for old laboratory notes, and pretty soon other crystals began to appear with seemingly impossible patterns, such as eight- and twelvefold symmetries.
When Shechtman had published his discovery, he still had no clear grasp of what the strange crystal actually looked like on the inside. Evidently its symmetry was fivefold, but how were the atoms packed? The answer to that question would come from unexpected quarters: mathematical games with mosaics.
The mosaics of explanation
Mathematicians like to challenge themselves with puzzles and logic problems. During the 1960s, they began to ponder whether a mosaic could be laid with a limited number of tiles so that the pattern never repeated itself, to create a so-called aperiodic mosaic. The first successful attempt was reported in 1966 by an American mathematician, but it required more than 20 000 different tiles and was thus far from pleasing mathematicians’ penchant for parsimony. As more and more people took on the challenge, the number of tiles required steadily shrank.
Finally, in the mid-1970s, a British professor of mathematics, Roger Penrose, provided a most elegant solution to the problem. He created aperiodic mosaics with just two different tiles, for example, a fat and a thin rhombus (figure 4:1).
Penrose’s mosaics inspired the scientific community in several different ways. Among other things, his findings have since been used to analyze medieval Islamic Girih patterns, and we have learned that Arabic artists produced aperiodic mosaics out of five unique tiles as early as the 13th century. Such mosaics decorate the extraordinary Alhambra Palace in Spain, for example, and portals and vaults of the Darb-i Imam Shrine in Iran.
The crystallographer Alan Mackay applied the Penrose mosaic in yet another manner. He was curious as to whether atoms, the building blocks of matter, could form aperiodic patterns like the mosaics. He conducted an experiment where he substituted circles, representing atoms, at intersections in the Penrose mosaic (figure 4:2). He then used this pattern as a diffraction grating in order to see what kind of diffraction pattern this would yield. The result was a tenfold symmetry – ten bright dots in a circle.
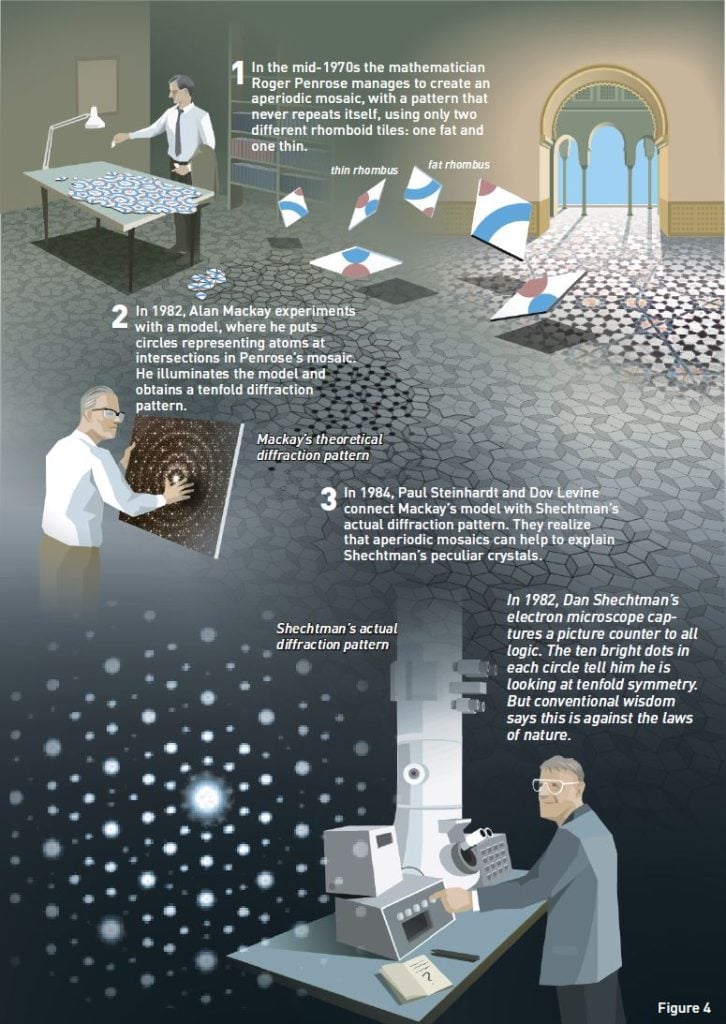
The connection between Mackay’s model and Shechtman’s diffraction pattern was subsequently made by the physicists Paul Steinhardt and Dov Levine. Before Shechtman’s article appeared in Physical Review Letters, the editor sent it off to other scientists for review. During this process, Steinhardt got the opportunity to read it. He was already acquainted with Mackay’s model, and realized that Mackay’s theoretical tenfold symmetry existed in real life in Shechtman’s laboratory at NIST.
On Christmas Eve, 1984, only five weeks after Shechtman’s article appeared in print, Steinhardt and Levine published an article where they described quasicrystals and their aperiodic mosaics. Quasicrystals got their name in this article.
The golden ratio – a key provided
A fascinating aspect of both quasicrystals and aperiodic mosaics is that the golden ratio of mathematics and art, the mathematical constant t (tau), occurs over and over again. For instance, the ratio between the numbers of fat and thin rhombi in Penrose’s mosaic is t. Similarly, the ratio of various distances between atoms in quasicrystals is always related to t.
The mathematical constant t is described by a sequence of numbers that the 13th-century Italian mathematician Fibonacci worked out from a hypothetical experiment dealing with rabbit reproduction. In this well-known sequence, each number is the sum of the two preceding numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc. If you divide one of the higher numbers in the Fibonacci sequence with the preceding number – for instance, 144/89 – you get a number that is close to the golden ratio.
Both the Fibonacci sequence and the golden ratio are important to scientists when they want to use a diffraction pattern to describe quasicrystals at the atomic level. The Fibonacci sequence can also explain how the discovery awarded the Nobel Prize in Chemistry 2011 has altered chemists’ conception of regularity in crystals.
Regularity without repetition
Previously, chemists interpreted regularity in crystals as a periodic and repeating pattern. However, the Fibonacci sequence is also regular, even though it never repeats itself, because it follows a mathematical rule. The interatomic distances in a quasicrystal correlate with the Fibonacci sequence; atoms are patterned in an orderly manner, and chemists can predict what a quasicrystal looks like on the inside. However, this regularity is not the same as when a crystal is periodic.
In 1992, this realization led the International Union of Crystallography to alter its definition of what a crystal is. Previously a crystal had been defined as “a substance in which the constituent atoms, molecules, or ions are packed in a regularly ordered, repeating three-dimensional pattern”. The new definition became “any solid having an essentially discrete diffraction diagram”. This definition is broader and allows for possible future discoveries of other kinds of crystals.
Quasicrystals in nature …
Since their discovery in 1982, hundreds of quasicrystals have been synthesized in laboratories around the world. Not until the summer of 2009, however, did scientists first report naturally occurring quasicrystals. They discovered a new kind of mineral in samples taken in the Khatyrka River in Eastern Russia. The mineral in question consists of aluminum, copper and iron, and yields a diffraction pattern with tenfold symmetry. It is called icosahedrite, after the icosahedron, a geometrical solid with sides consisting of 20 regular three-cornered polygons and with the golden ratio integrated into its geometry.
… and in highly resilient steel
Quasicrystals have also been found in one of the most durable kinds of steel in the world. When trying out different blends of metal, a Swedish company managed to create steel with many surprisingly good characteristics. Analyses of its atomic structure showed that it consists of two different phases: hard steel quasicrystals embedded in a softer kind of steel. The quasicrystals function as a kind of armor. This steel is now used in products such as razor blades and thin needles made specifically for eye surgery.
Despite being very hard, quasicrystals can fracture easily, like glass. Due to their unique atomic structure, they are also bad conductors of heat and electricity, and have non-stick surfaces. Their poor thermal transport properties may make them useful as so-called thermoelectric materials, which convert heat into electricity. The main purpose of developing such materials is to reuse waste heat, for example, from cars and trucks. Today, scientists also experiment with quasicrystals in surface coatings for frying pans, in components for energy-saving light-emitting diodes (LED), and for heat insulation in engines, among other things.
An important lesson for science
Dan Shechtman’s story is by no means unique. Over and over again in the history of science, researchers have been forced to do battle with established “truths”, which in hindsight have proven to be no more than mere assumptions. One of the fiercest critics of Dan Shechtman and his quasicrystals was Linus Pauling, himself a Nobel Laureate on two occasions. This clearly shows that even our greatest scientists are not immune to getting stuck in convention. Keeping an open mind and daring to question established knowledge may in fact be a scientist’s most important character traits.
Links and further reading
Websites
Shechtman, D., Technion – Israel Institute of Technology, http://materials.technion.ac.il/shechtman.html
Lifshitz, R., Introduction to quasicrystals, www.tau.ac.il/~ronlif/quasicrystals.html
Interviews and lectures (video and slide show)
Shechtman, D. (2010) Quasicrystals, a new form of matter, www.youtube.com/watch?v=EZRTzOMHQ4s
Senechal, M. (2011 ) Quasicrystals gifts to mathematics, www.youtube.com/watch?v=pjao3H4z7-g&feature=relmfu
Steurer, W. (2011 ) Fascinating quasicrystals, www.youtube.com/watch?v=jM4AIipGOdk
Steinhardt, P.J., What are quasicrystals?, www.physics.princeton.edu/~steinh/QuasiIntro.ppt
Popular science articles
Shtull-Trauring, A. (2011) Clear as crystal, Haaretz, www.haaretz.com/weekend/magazine/clear-as-crystal-1.353504
Scientific American, www.scientificamerican.com, search for quasicrystals.
Books
Hargittai, B. and Hargittai, I. (2005) Candid Science V: Conversations with Famous Scientists, Imperial College Press, London.
Original article
Shechtman, D., Blech, I., gratias, D., and Cahn, J.W. (1984) Metallic phase with long-range orientational order and no translational symmetry, Phys. Rev. Lett. 53(20):1951-1954.
The Laureate
DAN SHECHTMAN
Israeli citizen. Born 1941 in Tel Aviv, Israel. Ph.D. 1972 from Technion – Israel Institute of Technology, Haifa, Israel. Distinguished Professor, The Philip Tobias Chair, Technion – Israel Institute of Technology, Haifa, Israel.
Science Editors: Sven Lidin, Lars Thelander, The Nobel Committee for Chemistry
Text by Ann Fernholm
Illustrations: ©Johan Jarnestad/The Royal Swedish Academy of Sciences
Editor: Ann Fernholm
© The Royal Swedish Academy of Sciences
Nobel Prizes and laureates
Six prizes were awarded for achievements that have conferred the greatest benefit to humankind. The 12 laureates' work and discoveries range from proteins' structures and machine learning to fighting for a world free of nuclear weapons.
See them all presented here.
