Additional background material on the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel 1996

8 October 1996;

The Royal Swedish Academy of Sciences has decided to award the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel, 1996, to

Professor James A. Mirrlees, University of Cambridge, U.K. and
Professor William Vickrey, Columbia University, New York, USA
(deceased October 10, 1996)

for their fundamental contributions to the economic theory of incentives under asymmetric information.

Information and Incentives
One of the most important and liveliest areas of economic research in recent years addresses situations where decision-makers have different information. Such informational asymmetries occur in a great many contexts. For example, a bank does not have complete information about lenders’ future income; the owners of a firm may not have the same detailed information about costs and competitive conditions as the managing director; an insurance company cannot fully observe policyholders’ responsibility for insured property and external events which affect the risk of damage; an auctioneer does not have complete information about the willingness to pay of potential buyers; the government has to devise an income tax system without much knowledge about the productivity of individual citizens; etc.

Incomplete and asymmetrically distributed information has fundamental consequences, particularly in the sense that an informational advantage can often be exploited strategically. Research on the economics of information has therefore focused on the question of how contracts and institutions can be designed to handle different incentive and control problems. This has generated a better understanding of insurance markets, credit markets, auctions, the internal organization of firms, wage forms, tax systems, social insurance, competitive conditions, political institutions, etc.

This year’s laureates have laid the foundation for examining these seemingly quite disparate areas through their analytical work on issues where informational asymmetries are a key component. An essential part of William Vickrey‘s research has concerned the properties of different types of auctions, and how they can best be designed so as to generate economic efficiency. His endeavors have provided the basis for a lively field of research which, more recently, has also been extended to practical applications such as auctions of treasury bonds and band spectrum licenses. In the mid 1940s, Vickrey also formulated a model indicating how income taxation can be designed to attain a balance between efficiency and equity. A quarter of a century later, interest in this model was renewed when James Mirrlees found a more complete solution to the problems associated with optimal income taxes. Mirrlees soon realized that his method could also be applied to many other similar problems. It has become a principal constituent of the modern analysis of complex information and incentive problems.

1. William Vickrey
William Vickrey was born in 1914 in Victoria, British Columbia. He received his Bachelor of Science degree from Yale University in 1935. That same year, he began his postgraduate studies at Columbia University, New York, where he received his Master’s degree in 1937 and his Ph.D. in 1947. He has been affiliated with the faculty of Columbia University since 1946, and served as a tax advisor for various organizations between 1937 and 1947. He was Professor Emeritus at Columbia University.

Throughout his professional life, Vickrey was engaged primarily in research and teaching; he was also appointed to fact-finding commissions by a number of public authorities. For example, he designed a fare system for the New York subway (1951) and worked on city planning and transportation in India, Argentina and Venezuela (1962-63). Among Vickrey’s better-known activities as a consultant are also his studies of the transportation and traffic system in Washington DC in the late 1950s and his service as an advisor to the UN on taxation.

William Vickrey has above all contributed to enhancing our knowledge about the efficient use of resources in the public sector. Notwithstanding his numerous and far-reaching practical applications, it is the depth of his theoretical endeavors which gives lasting value to his scientific lifework. Vickrey has a characteristic style of writing; almost in passing, he interposes deep insights in seemingly routine economic arguments. This has sometimes inferred that his theoretical contributions did not become apparent until long after they were written. Vickrey’s creativity is particularly remarkable in his studies of social choice and resource allocation mechanisms. He has also carried out important research on public-sector pricing as well as transportation and urban economics.

1.1. Auctions and Resource Allocation
One of Vickrey’s foremost contributions is his article “Counterspeculation, Auctions, and Competitive Sealed Tenders” (1961), where he analyzed different kinds of auctions and introduced the so-called second-price auction or, as it came to be known, the Vickrey auction. His study was inspired by Abba P. Lerner’s suggestion that, in markets with imperfect competition, efficiency-enhancing institutions should be developed so as to generate a resource allocation similar to that under perfect competition. Vickrey’s analysis proved important not only to the theory of auctions, but also in providing general insights into the design of allocation mechanisms aimed at creating socially desirable incentives when information is incomplete. It is related, for example, to the problem of inducing people to state their true willingness to pay for public services.

In a second-price auction, an object (a resource, a right) is auctioned off by means of sealed bidding, where the highest bidder gets to buy the item, but at the second highest bid. This mechanism elicits the individual’s true willingness to pay. By bidding above his own willingness to pay, an individual runs the risk that someone else will bid likewise, and he could be forced to buy the object at a loss. If he instead bids below his own willingness to pay, he runs the risk of someone else buying the item at a lower price than the amount he himself is willing to pay. In this type of auction, a truthful bid is thus the dominant strategy. The auction also distributes the good in a socially, efficient way; the object goes to the bidder with the highest willingness to pay, and the bidder in question pays the social opportunity cost which is the second highest bid.

An analogous idea underlies the so-called Clarke-Groves mechanism for eliciting truthful tenders for public projects, which was worked out in detail by Clarke (1971) and Groves and Loeb (1975). Vickrey anticipated this important result by a substantial time margin.

The efficiency aspect was Vickrey’s main interest when the second-price auction was introduced in his 1961 article. Another issue that interested him is which type of auction would yield the highest expected price. Apart from the Vickrey auction, he studied three other auctions. An English auction begins with the auctioneer requesting a first bid, and ends when he can no longer elicit a higher bid. The object goes to the highest bidder, who pays his tender. A Dutch auction starts at a price which far surpasses the amount any of the participants are willing to pay. The price is gradually reduced until someone shouts “mine” and then gets to buy the object at the proposed price. A first-price auction relies on sealed bidding, where the highest bidder buys the good at his tendered price.

Vickrey noted that the English auction and the second-price auction are strategically equivalent and, likewise, that the Dutch auction and the first-price auction are strategically equivalent. He also showed that if bidders’ valuations of the object are statistically independent and uniformly distributed over an interval, then – in Nash equilibrium – all four auctions result in the same expected price paid to the seller. This important finding has later been extended and has become known as the revenue equivalence theorem.

A distinguishing feature of the second-price (and hence also the English) auction is that it only requires individual rationality. That is, a participant’s optimal bid in such an auction is independent of his expectations about others’ bids. This contrasts with the first-price (and hence also the Dutch) auction, in which optimality depends on (equilibrium) expectations, making the outcome less robust.

In his article “Auctions and Bidding Games” (1962), Vickrey elaborated on the game-theoretic aspects of auctions, and generalized his earlier analysis to auctions over multiple (identical) objects as well as to a broader class of distributions for the willingness to pay.

In his work on auctions, Vickrey studied games under first-order incomplete information, thereby anticipating the 1994 economics laureate John Harsanyi’s more thorough research on games with incomplete information.¹ In recent years, analysis of auctions as allocation mechanisms has become a very active field of research.

1. Incomplete information of the first order arises in an auction game if i) the bidders do not know one another’s willingness to pay, but instead assign probability distributions to them, and ii) the bidders know these probability distributions. Incomplete information of higher orders implies, roughly speaking, that the bidders have expectations about each other’s expectations, etc.

1.2. Optimal Income Taxation
Vickrey’s most creative endeavor regarding taxation is his article “Measuring Marginal Utility by Reactions to Risk” (1945), which addresses the balance between efficiency and equity in designing an income tax system. It is explicitly formulated in the form of – what economists now call – an optimal income tax problem.

Edgeworth’s classical essay (1897) on the structure of income taxation is based on a utilitarian welfare perspective. His intention was to examine how a system of redistributive taxes should be designed in order to maximize social welfare, defined as the sum of all individuals’ utility (welfare). Assuming diminishing marginal utility of consumption, he found support for a progressive tax schedule. If all individuals derive the same utility from consumption, a welfare optimum requires the marginal utility of consumption to be the same for all individuals. If their gross incomes differ, then net income has to be equalized.

Vickrey (1945) emphasized that such taxation does not give individuals incentives to work. His analysis takes the same utilitarian approach as Edgeworth did; the government wants to maximize the sum of all individuals’ utility. Vickrey assumes that all individuals have the same preferences over productive effort e and consumption y, but different abilities to produce goods and services. He also assumes that the productive effort e required of an individual with ability t to produce quantity x is given by a function w, or e = w(x,t).

The government’s aim is to maximize the sum of all individuals’ utility, given that total tax revenue reaches a predetermined level. Vickrey presupposes that redistribution takes place by means of a tax function f which determines each individual’s consumption y based on his production x, that is, by the equation y = f(x). The tax paid is thus x-y. Given the tax function f, each individual t chooses his production x so that his utility is maximized. Let x*(t) be individual t‘s optimal choice of productive effort, and let v(t) be the resulting (maximum) utility level for the individual.

The objective of the government’s choice is the function f, where f is chosen so that the “sum”²

(1) v(t)dt

of all individual’s utility is maximized, under the constraint that the total tax revenue

(2) (x*(t) -f(x*(t)))dt

is equal to a given level. Vickrey derived the so-called Euler equation for this calculus of variation problem, a necessary condition for an optimal tax function. But the equation became implicit and rather complicated; Vickrey concluded the formal part of the discussion by declaring: “Expanding this expression…produces a completely unwieldy expression. Thus even in this simplified form the problem resists any facile solution.” As it turned out, this conclusion was too pessimistic.

In his paper “The Problem of Progression” (1968), Vickrey returned to the problem of creating the right balance between incentives and distributional objectives in the income tax system, although he was not able to specify the degree of progressivity in the optimal tax structure. He also considered the technical and political difficulties in constructing a tax system which is progressive in any real sense.

It proved to be James Mirrlees who, independently of Vickrey’s article from 1945, gave the optimal income tax problem a new and precise formulation and developed a methodology for analyzing the properties of the solution (see Section 2.1).

2. For technical reasons, Vickrey chose to treat the population as a continuum, whereby sums can be replaced by more manageable integrals.

1.3. Other Contributions
The above-mentioned article from 1945 contains another pioneering theoretical contribution. While considering methods of measuring utility through individuals’ decisions under uncertainty, Vickrey introduced the approach of letting the individual himself evaluate income distributions by assuming that he can, with equal probability, end up in any other individual’s position in the distribution. This approach, where societies are evaluated under the veil of ignorance, was later rediscovered and developed by John Harsanyi in two studies in the early 1950s (1953, 1955), where he introduced the concept of the original position. The same idea is taken up in John Rawls’s book, A Theory of Justice (1971).³

In his paper “Utility, Strategy, and Social Decision Rules” (1960), Vickrey discusses Kenneth Arrow’s impossibility theorem and corrects an error in Arrow’s analysis. He also asserted that the condition that the preference ordering should be independent of irrelevant alternatives is sufficient for ensuring that a voting procedure will not be manipulable, in the sense that no one should be able to sway the outcome of the vote to his advantage by stating untruthful preferences. Since Arrow showed that all of his conditions are impossible to fulfill simultaneously, Vickrey guessed, perceptively, that a voting procedure which fulfils the remaining requirements is manipulable. Almost 15 years later, Allan Gibbard (1973) and Mark Satterthwaite (1975) succeeded in showing that Vickrey had been right. According to Gibbard: “Indeed the proof in this paper proceeds roughly by confirming Vickrey’s conjecture.” More specifically, they demonstrated that every voting procedure, which is not determined by a dictator and has at least three outcomes, is manipulable. In the literature, this is known as the Gibbard-Satterthwaite impossibility theorem.

Vickrey’s doctoral thesis, “An Agenda for Progressive Taxation”, was published in 1947. The agenda consists of 21 proposals for reforming the U.S. income tax system. His objective was to design a stable tax base, which he regarded as a prerequisite for a progressive tax system. His dissertation contains an innovation which is quite likely to be part of economists’ intellectual baggage for a long time. In fact, the concept of cumulative averaging was first presented in Vickrey’s article “Averaging of Income for Tax Purposes” (1939). The idea is that taxation should be neutral with respect to the point in time when income is realized, which eliminates the incentive for taxpayers to vary transaction times for tax purposes. Once the principle was formulated, consistent logic and practical considerations remained. Vickrey found the sought-after neutrality by regarding all tax payments as deposits in an interest-bearing account in the taxpayer’s name. Under these conditions, the tax owed at a certain point in time would be equal to the tax on the total income accumulated, including the interest income on the tax account, minus the accumulated tax already deposited in the account. The idea was never put into practice, however.⁴

Marginal cost pricing of public services permeates Vickrey’s scientific production. About 40 of his studies address efficient pricing of public services. He has not only made significant theoretical contributions but, unlike most excellent theorists, he has also followed up on his proposals all the way to their implementation.

A problem with marginal cost pricing in public enterprises is that full cost coverage cannot be attained if the marginal cost decreases with the volume of production. This problem had already been dealt with in 1926 by Frank Ramsey, who solved the pricing problem under a given budget restriction. The solution is called Ramsey pricing and implies, roughly speaking, that prices are inversely proportional to the price elasticity of the demand for the various goods.

In his classical inquiry into pricing of subway transportation in New York, “A Proposal for Revising New York’s Subway Fare System” (1955), Vickrey realized that marginal cost pricing would burden the subway system with a substantial budget deficit, which would have to be covered through taxation. Since taxes have a social cost in that they distort incentives, he tried to estimate the marginal cost of the additional taxes required to cover the deficit. The fare should then be set so as to achieve a balance between the social losses from raising the price above the marginal cost and the subsequent gains from lessening the need for tax revenue. The analysis is an early example of how Ramsey pricing can be implemented in practice. It also improved on Ramsey’s original representation of the problem; Vickrey evaluated pricing policy against the marginal cost of tax revenue and not against a given budget restriction.

Characteristically, Vickrey’s New York study also contains some interesting practical details. For instance, he suggested that each passenger should pay a maximum fare (25 cents) when boarding the subway, using a ticket magnetically coded with the time and place. When exiting, the passenger would insert the ticket in a turnstile and be refunded the difference between the maximum fare and the real cost.

Vickrey has also done other work in urban economics, the most important of which is perhaps his article entitled “Congestion Theory and Transport Investment” (1969). The model is relatively simple. A group of commuters who start work at the same time have to pass a “bottleneck” on their way to the office. If the number of arrivals at the bottleneck exceeds its capacity, a line develops. When the commuters decide what time to leave home, they weigh the gains in travel time against the costs of getting up too early or arriving late for work. Vickrey realized that travel costs in equilibrium are independent of when the journey begins. In other words, the cost of getting up early for the commuter who leaves home first is equal to the cost of standing in line at the bottleneck for the commuter who gets to work on time. Under different road tariff systems, applications of this equilibrium concept allow a solution for determining the length of the queue over time and an equilibrium pattern for departure times. Vickrey showed that the equilibrium tariff can be used for profitable “tax switching”. Commuters are by definition indifferent between paying a road toll and not having to stand in line, or not paying a toll and standing in line. What is more, there is no change in arrival times at work. Hence, the tax has neither excess burden nor burden, and the tax revenue can be used to reduce other tolls for motorists, thereby improving their situation. As usual, Vickrey was ahead of his time. His model was rediscovered by road engineers and economists in the early 1980s.

3. Vickrey returned to the veil of ignorance in other respects before Rawls had finished his book; see Vickrey (1968).

4. An incomplete predecessor was the income tax system in Wisconsin during the period 1928-1932.

2. James A. Mirrlees
James A. Mirrlees was born in 1936 in Minnigaff, Scotland. He received his Master’s degree in Mathematics in Edinburgh in 1957, and his Ph.D. from the University of Cambridge in 1963. He was Edgeworth Professor of Economics at Oxford University between 1969 and 1995, and currently holds a professorship in Economics at the University of Cambridge.

Mirrlees has made several far-reaching contributions in public economics, particularly in optimal taxation and development. One of his most important contributions, carried out jointly with Peter Diamond, consists of a very thorough and almost definitive treatment of optimal commodity taxes (see Section 2.3). Mirrlees subsequently applied this production efficiency result in analyses, coauthored with Ian Little, of cost-benefit rules in developing economies. These rules have since become common property in economics. Mirrlees’s foremost achievement, however, is related to information and incentive theory. His study of optimal income taxes was the first complete analysis of the optimal design of economic policy under information asymmetries. In solving this problem, he developed a methodology which has become a paradigm in the economics of asymmetric information.

2.1. Optimal Income Taxation
Mirrlees’s model for optimal income taxation is very similar to Vickrey’s. It is assumed that the government’s objective is to maximize the sum of all individuals’ utility, and all individuals have the same preferences for leisure and consumption, but different abilities to produce goods and services. Individuals know their productivity, but this information is not shared by the government.

As in the description of Vickrey’s model, let x denote an individual’s pretax income, or production, and y his aftertax income, or consumption. Individual differences in productivity are captured by an index t distributed over some interval. An individual with a higher t can produce a given quantity x of goods and services with less effort or in less working hours. Let the scale for t be such that an individual of type t with productivity e, for example measured in the number of working hours per week, produces x = et; this corresponds to e = w(x,t) = x/t in Vickrey’s analysis. The utility of an individual who consumes c and works e is u(c,e), where the utility function u is assumed to be increasing in its first argument and decreasing in its second. By normalizing the length of the workweek to 1, the residual z = 1-e represents the individual’s leisure.

The government’s objective is to maximize the sum of all individuals’ utility under the constraint that their combined consumption does not exceed total production.⁵ If the government could observe each individual’s type t, then it would only have to require each individual to produce and consume in accordance with the solution to this optimization problem. If leisure is a normal good (i.e., the individual chooses to consume more of it with rising income), the solution would result in lower utility for individuals with a higher productivity index. This follows from the fact that the government on the one hand wants to equate individual differences in the marginal utility of consumption (so as to maximize the sum of their utility), while, on the other hand, it wants to require more productive individuals to work more (so as to facilitate meeting the resource restriction). At the optimum, the balance between these two objectives would imply a transfer of utility from more to less productive individuals.

The fact that the resulting individual utility would be decreasing in the productivity index illustrates the underlying incentive problem: if the government cannot observe an individual’s type t and would attempt to implement the above solution, it would be in the self-interest of all individuals to claim that their productivity is lower than is actually the case. The first-best solution outlined here is therefore not feasible when individuals’ productivity is their private information. Instead, Mirrlees tried to find a second-best solution presupposing that individuals’ productivity is in fact their own private information, and that redistribution has to take place through a tax schedule common to all individuals. Just as in Vickrey’s model, the tax schedule determines aftertax income y as a function f of pretax income x. Given such a tax function f, each type of individual t chooses his pretax income (production) x in order to achieve maximum utility u(f(x),x/t). For individual t, let x*(t) and y*(t) be the optimal choice of own production and consumption, and let v(t) be his resulting (maximum) utility.

The individual’s utility maximization problem is shown in Figure 1. The horizontal axis represents the individual’s production, x = et, and the vertical axis his consumption y. The dashed curves designate levels of the utility function u, and the solid irregular line is the tax function f. The upper bound on working hours e is normalized to 1, so that the upper bound on t‘s production is t. The shaded area under the graph of the tax function is the individual’s choice set. The optimal utility level v(t) is achieved at the point (indicated in the figure) where the highest level curve which intersects the choice set is tangent to the tax function (the boundary of the choice set).

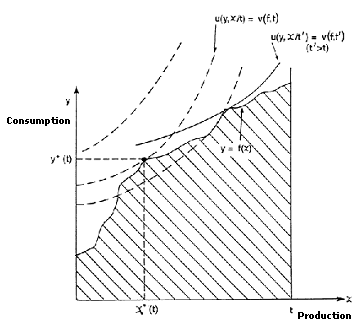Figure 1. The utility maximization problem for an individual of arbitrary type t.

The tax schedule f is thus the object of the government’s choice, i.e., its policy instrument. Each property of the tax schedule, such as its progressivity, has to be derived from the government’s optimization problem; none of these properties can be assumed at the outset. This implies, for instance, that the usual convexity assumptions which are crucial in economic models cannot be made.⁶ Owing to this circumstance, the government’s optimization problem, containing all individuals’ optimization problems as constraints, becomes unwieldy.

Mirrlees’s breakthrough was to impose an empirically reasonable restriction on the utility function. Under this restriction, the government’s optimization problem can be reformulated so that the constraint incorporating all individuals’ optimization problems can be replaced by a differential equation for the utility derivative dv(t)/dt. This equation indicates how the resulting individual utility level changes when there is a marginal change in the type of individual t. Mirrlees made the astute observation that this optimization problem may be regarded as a dynamic control problem of a type that is well known from applied mathematics. He interpreted t as “time”, the utility level v(t) as the “state” at time t, the differential equation as the “law of motion” for the state variable v(t), and individual t‘s production x(t) as the control variable. He then proceeded to solve this dynamic control problem using Pontryagin’s maximum principle.

The solution to the optimization problem, the quantities 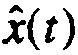and 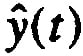for each type of individual t, can be respecified as a tax function, y = f(x), by eliminating the index t from the set of equations y = and x =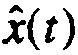. The government’s optimal policy instrument f under asymmetric information can then be identified.

Mirrlees showed that the differential equation for v(t) guarantees an outcome whereby each type of individual t will choose the production 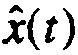which is optimal from the government’s point of view, that is, x*(t) = .

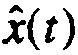This approach has subsequently been applied in several basic models with asymmetric information. In general, however, there is no analytical solution; instead, the optimal tax function has to be obtained by numerical methods. Here, of course, the degree of progressivity will be lower than it is according to Edgeworth’s result. In some income intervals, the result can even be a regressive tax schedule.

The key assumption that enables this drastic simplification and reformulation of the optimization problem is the so-called single-crossing condition. The essential requirement of this condition with respect to the utility function u is that if two level curves in the (x,y) plane, one for individual t and the other for individual t’, intersect, then the level curve for the more productive individual has a smaller slope; see Figure 1. In other words, two level curves cannot intersect more than once – thereof the name of the condition. In relation to an (increasing) tax function f, this implies that more productive individuals will find it optimal to produce more; cf. Figure 1. In more economic terms, the essential requirement of this condition is that if increased effort is imposed on an individual, then in order for the individual to remain indifferent, he needs a greater increase in consumption as compensation, the higher his initial effort. The single-crossing condition has become central to several microeconomic and game theoretic models of incentives under asymmetric information. Mirrlees was the first to identify the condition and explain its analytical significance.

The optimization problem respecified by Mirrlees yields the same result as if the government had asked all individuals to report their productivity index t, and had then imposed corresponding production and consumption objectives, 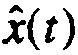and . These individual objectives, stated in advance for each productivity index t, would constitute a binding commitment on the part of the government as to how the private information reported by individuals would be used. Given this commitment from the government, every individual would fulfill his objective voluntarily.

Mirrlees’s analysis thus proved to contain the germ of a very profound and general insight. An economic allocation mechanism which asks all individuals to provide their private information is called direct. If truthful reporting is optimal for all individuals, the mechanism is called incentive compatible. The above argument indicates that the allocations which can be achieved through a tax function f under the single-crossing condition can be attained by a direct and incentive-compatible allocation mechanism. The so-called revelation principle signifies that for every desired allocation, there is a direct and incentive-compatible mechanism which implements it.⁷ This principle allows the analyst to limit the search for an optimal mechanism to the relatively small subclass of direct and incentive-compatible mechanisms. It usually represents a considerable simplification of the analytical problem. Other researchers later developed a general form of the revelation principle, which has had a far-reaching influence on microeconomic theory; cf. e.g. Dasgupta, Hammond and Maskin (1979) and Myerson (1982). Nowadays, it is the standard method for designing optimal allocation mechanisms under asymmetric information.

Early applications of the methodology in Mirrlees (1971) may be found in Spence and Zeckhauser (1971) on health insurance, Sheshinski (1972) on linear income taxation, Spence (1977) on nonlinear pricing, and Mussa and Rosen (1978) on product quality, etc.

5. Since it is assumed that there is a continuum of types of individuals, the sums take the analytical form of integrals over the type index t.

6. In Figure 1, note that since there is more than one tangential point between the level curves and the graph of the tax function, multiple optima can be obtained for individuals. This would not be possible under conventional convexity assumptions.

7. The equilibrium condition for implementing the mechanism is important in this context. In Mirrlees’s model, the desired allocation can be effectuated under the weakest equilibrium condition used, i.e., “solution in undominated strategies”. This is also the case in the Vickrey auction; see Section 1.1.

2.2. Moral Hazard
The informational asymmetry in optimal taxation concerns both the type t of the individual and his or her work effort e. In Mirrlees’s model, the government is only assumed to know the product x = te. Another type of incentive problem is dealt with in the above-mentioned paper by Spence and Zeckhauser regarding the optimal design of health insurance. This is usually referred to as moral hazard. In a series of studies during the 1970s, Mirrlees analyzed this kind of problem, with applications to insurance and to incentives in organizations and firms.

A moral-hazard problem between two parties is comprised of: a variable x, which is observable to both parties; the “outcome”, which depends on one party’s – the agent‘s – action a, which the other party – the principal – cannot observe; and a stochastic variable . The outcome x is thus a function of a and ; x = g(a, ).⁸ In an insurance context, where the term moral hazard originated, can be some potentially harmful effect on the object (such as weather or attempted theft), a the care taken by the policyholder, and x the resulting damages to the object. In the relation between the owners and the management of a firm, a can be the executive’s work effort, x profits, and production and market conditions. In both cases, represents external factors which may be difficult or impossible for the principal to monitor.

Following the 1972 economics laureate Kenneth Arrow (1963), moral-hazard problems have been modelled in exactly this way; see e.g. Spence and Zeckhauser (1971). However, severe technical problems have been encountered, similar to those noted by Vickrey in connection with optimal income taxation. The approach was too cumbersome. Mirrlees realized that each action carried out by the agent gives rise to a probability distribution over the outcomes. The agent’s choice of action can thus be regarded as a choice of probability distribution. This seemingly simple reformulation turned out to permit a more powerful analysis. Mirrlees proceeded to develop this reasoning in a series of papers (1974,1975, 1976, 1979).

According to the terminology currently used in this area, a contract between an economic agent and a principal is a rule, or function h, which for every outcome x indicates (positive or negative) compensation y to the agent: y = h(x). Here, the compensation rule h is the object of the principal’s choice – in the same way that the tax schedule f is the government’s choice in income taxation. The principal (the insurance company or the owner of a firm) is assumed to choose the compensation rule with the objective of maximizing his own expected utility, under two constraints. First, since the contract relation is assumed to be voluntary, the principal has to ensure that the agent is willing to accept the contract, i.e., choose the function h so that the agent has at least as high expected utility from accepting the contract as from rejecting it. This is known as the incentive compatibility constraint or the participation constraint. The second constraint is that once the agent has signed the contract, his action a is optimal for him under the contract.

As in the case of the income tax schedule f, analytically desirable properties of the function h cannot be assumed at the outset; they have to be derived from the optimality conditions.⁹ Again, there is an obstacle to further analysis, and once again it was Mirrlees who was able to overcome it.

He began by replacing the agent’s optimality constraint with an equation expressing a first-order condition for the agent’s action to be optimal. When this equation is inserted into the principal’s first-order condition, the resulting equation contains the ratio between both parties’ marginal utility. This ratio had already appeared in the earlier Arrow-Debreu model of optimal risk sharing under symmetric information, i.e., without the informational asymmetry outlined here. Mirrlees’s equation also contains a new term which can be interpreted as the derivative of a likelihood ratio. Let (x|a) be the probability density of the outcome x, given the agent’s action a. This can be written as the derivative of the logarithm of (x|a) with respect to a. The term expresses the information about the agent’s action contained in the outcome x, and thus the extent to which risk sharing has to be restricted because information is asymmetric to the disadvantage of the principal.

This is where Mirrlees’s reinterpretation of the agent’s choice – from a choice of action a to a choice of distribution function for the outcome x – becomes crucial. This interpretation can be used to determine the cost of compensating the agent so that his effort will come close to that which is optimal for the principal. Mirrlees showed that it is cheap for the principal to implement the desired outcome if the agent is sensitive to “punishment” (low or negative compensation) and if, in addition, the derivative above becomes very large in bad outcomes. The optimal contract will then approximate the solution to the Arrow-Debreu first-best solution under symmetric information. This occurs simply by letting the contract stipulate severe punishment in bad outcomes. The result is that the policyholder takes care of the insured object almost as if it were uninsured, and the executive manages the firm almost as if it were his own. Under the above assumptions, bad outcomes are in fact highly informative; the principal knows almost for certain that the agent has not exerted himself to any large extent. Mirrlees (1974) provided similar examples, and Mirrlees (1975, 1976) established general results.

Prior to Mirrlees, other researchers had replaced the agent’s optimality conditions with an equation for first-order conditions; see e.g. Ross (1973). But it was Mirrlees (1975) who showed that this method – which in general only yields a necessary but not sufficient condition for optimality, and can be applied only if the function h is “well behaved” – is problematic. As in the case of nonlinear optimal taxation, nonlinear contracts easily lead to nonconvexities. Mirrlees identified two conditions which allow the first-order aspect to be applied: the monotone likelihood ratio and the convex distribution function property.

8. This function g and the probability distribution of are assumed to be common knowledge– to both parties. In the standard model, it is assumed that the agent does not know the value of when he chooses action a.

9. In general, the optimal reward is not even monotonically related to the outcome.

2.3. Other Contributions
Mirrlees (1976) applied the method sketched above to the internal organization of firms, with an emphasis on incentive pay schemes and hierarchical structures. This work contributed substantially to formalizing the 1991 economics laureate Ronald Coase’s insight that the size of a firm is determined by a balance between the costs of internal control and the costs of market transactions. A noteworthy result of Mirrlees’s analysis is that compensation at lower levels in a firm should take the form of fixed wages, whereas profit-related pay is preferable at top management levels.

In collaboration with Peter Diamond, Mirrlees has also carried out a comprehensive analysis of commodity taxes in a second-best world. Due to the fact that commodity taxes create a “tax wedge” between consumer and producer prices, taxpayers are prepared to pay more in order to avoid the taxes than the amount which accrues to the government in tax revenue. Given that this social cost cannot be fully prevented, taxes have to be chosen in the second-best way.

The general theory of optimal taxation in a second-best economy encompasses few clear-cut recommendations. If one condition for social efficiency is violated, as a rule there is reason to violate others as well. However, Diamond and Mirrlees (1971) obtained a highly universal result. Under relatively general conditions, it is desirable to maintain production efficiency. In concrete terms, this means that taxes should not be levied on factors of production.

The underlying intuition is relatively simple. Assume that final consumption varies continuously with tax rates. Diamond and Mirrlees showed that, in general, there exists a change in the tax rates which is advantageous to all consumers. If production is not efficient at the outset, i.e., it is in the interior of the production set, there will be a sufficiently small change in tax rates which is favorable to all consumers and still keeps the economy within the production set (due to continuity). Hence, the initial situation could not have been optimal.

As already indicated, this result has had widespread consequences for project appraisal and economic policy in developing countries. Jointly with Little, Mirrlees has set up criteria for evaluating projects based on the desirability of efficiency in production; see Little and Mirrlees (1974). On a theoretical level, the analysis has been generalized in various directions in Mirrlees (1972) and Diamond and Mirrlees (1976).

3. Summary Statement
James A. Mirrlees and William Vickrey have been awarded the 1996 Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel for their fundamental contributions to the economic theory of incentives under asymmetric information.

4. References
Arrow, K.J., (1963) Uncertainty and the Welfare Economics of Medical Care, American Economic Review 53, 941-969.

Clarke, E., (1971) Multipart Pricing of Public Goods, Public Choice 8, 19-33.

Dasgupta, P.S., Hammond, P.J., and Maskin, E., (1979) The Implementation of Social Choice Rules: Some General Results on Incentive Compatibility, Review of Economic Studies 46, 185-216.

Diamond, P., and Mirrlees, J.A., (1971) Optimal Taxation and Public Production I: Production Efficiency, II: Tax Rules, American Economic Review 61, 8-27, and 261-278.

Diamond, P., and Mirrlees, J.A.,(1976) Private Constant Returns and Public Shadow Prices, Review of Economic Studies 43, 41-78.

Edgeworth, F.Y., (1897) The Pure Theory of Taxation, Economic Journal 7, 46-70, 226-238 och 550-571.

Gibbard, A., (1972) Manipulation of Voting Schemes: A General Result, Econometrica 41, 587-601.

Groves, T., and Loeb, M., (1975) Incentives and Public Inputs, Journal of Public Economics 4, 311-326.

Harsanyi, J., (1953) Cardinal Utility in Welfare Economics and in the Theory of Risk Taking, Journal of Political Economy 61, 434-435.

Harsanyi, J., (1955) Cardinal Welfare, Individalistic Ethics, and Interpersonal Comparisons of Utility, Journal of Political Economy 63, 309-321

Little, I.M.D., and Mirrlees, J.A., (1974) Project Appraisal and Planning for Developing Countries, New York: Basic Books.

Mirrlees, J.A., (1971) An Exploration in the Theory of Optimal Income Taxation,

Review of Economic Studies 38, 175-208. Mirrlees, J.A., (1972) On Producer Taxation, Review of Economic Studies 39, 105-111.

Mirrlees, J.A., (1974) Notes on Welfare Economics, Information and Uncertainty, in Balch, M., Mc Fadden, D., and Wu, S., (eds.) Essays in Equilibrium Behavior, Amsterdam: North Holland.

Mirrlees, J.A., (1975) The Theory of Moral Hazard and Unobservable Behavior: Part I, Nuffield College, Oxford, mimeographed.

Mirrlees, J.A., (1976) The Optimal Structure of Incentives and Authority within an Organisation, Bell Journal of Economics 7 , 105-131.

Mirrlees, J.A., (1979) The Implications of Moral Hazard for Optimal Insurance, paper presented at a symposium in honor of Karl Borch, Uncertainty and Insurance in Economic Theory, Bergen.

Mussa, M., and Rosen, S., (1978) Monopoly and Product Quality, Journal of Economic Theory 18, 301-307.

Myerson, R., (1982) Optimal Coordination Mechanisms in Generalized Principal-Agent Problems,

Journal of Mathematical Economics 10, 67-81. Rawls, J., The Theory of Justice, Boston: Harvard University Press.

Ross, S., (1973) The Economic Theory of Agency: The Principals Problem, American Economic Review 63, 134-139.

Satterthwaite, M., (1975) Strategy Proofness and Arrows Conditions: Existence and Correspondence Theorems for Voting Procedures and Social Welfare Functions, Journal of Economic Theory 10, 187-217.

Sheshinski, E., (1972) The Optimal Linear Income Tax, Review of Economic Studies 39, 179-208.

Spence, M.,(1977) Non-Linear Prices and Economic Welfare, Journal of Public Economics 8, 1-18.

Spence, M., and Zeckhauser, R., (1971) Insurance, Information, and Individual Action, American Economic Review 61, 380-387.

Vickrey, W., (1939) Averaging of Income for Income Tax Purposes, Journal of Political Economy 47, 379-397.

Vickrey, W., (1945) Measuring Marginal Utility by Reactions to Risk, Econometrica 13, 319-333.

Vickrey, W., (1947) An Agenda for Progessive Taxation, New York: Ronald Press.

Vickrey, W., (1955) A Proposal for Revising New Yorks Subway Fare System, Journal of The Operations Research Society of America 3, 38-69.

Vickrey, W., (1960) Utility, Strategy, and Social Decision Rules, Quarterly Journal of Economics 74, 507-535.

Vickrey, W., (1961) Counterspeculation, Auctions, and Competitive Sealed Tenders, Journal of Finance 16, 8-37.

Vickrey, W., (1962) Auction and Bidding Games, in Recent Advances in Game Theory, Proceedings of a Conference, Princeton: Princeton University Press.

Vickrey, W., (1968) The Problem of Progression, University of Florida Law Review, 437-450.

Vickrey, W., (1969) Congestion Theory and Transport Investment, American Economic Review 59, 251-260.