Advanced information

Additional background material on the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel 1997
14 October 1997
The Royal Swedish Academy of Sciences has decided to award the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel 1997, to
Professor Robert C. Merton, Harvard University, and
Professor Myron S. Scholes, Stanford University
for a new method to determine the value of derivatives.
Risk management is essential in a modern market economy. Financial markets enable firms and households to select an appropriate level of risk in their transactions, by redistributing risks towards other agents who are willing and able to assume them. Markets for options, futures and other so-called derivative securities – derivatives, for short – have a particular status. Futures allow agents to hedge against upcoming risks; such contracts promise future delivery of a certain item at a certain price. As an example, a firm might decide to engage in copper mining after determining that the metal to be extracted can be sold in advance at the futures market for copper. The risk of future movements in the copper price is thereby transferred from the owner of the mine to the buyer of the contract. Due to their design, options allow agents to hedge against one-sided risks; options give the right, but not the obligation, to buy or sell something at a pre-specified price in the future. An importing British firm that anticipates making a large payment in US dollars can hedge against the one-sided risk of large losses due to a future depreciation of sterling by buying call options for dollars on the market for foreign currency options. Effective risk management requires that such instruments be correctly priced.
Fischer Black, Robert Merton and Myron Scholes made a pioneering contribution to economic sciences by developing a new method of determining the value of derivatives. Their innovative work in the early 1970s, which solved a longstanding problem in financial economics, has provided us with completely new ways of dealing with financial risk, both in theory and in practice. Their method has contributed substantially to the rapid growth of markets for derivatives in the last two decades. Fischer Black died in his early fifties in August 1995.
Black, Merton and Scholes´ contribution extends far beyond the pricing of derivatives, however. Whereas most existing options are financial, a number of economic contracts and decisions can also be viewed as options: an investment in buildings and machinery may provide opportunities (options) to expand into new markets in the future. Their methodology has proven general enough for a wide range of applications. It can thus be used to value not only the flexibility of physical investment projects but also insurance contracts and guarantees. It has created new areas of research – inside as well as outside of financial economics.
The history of option valuation
Attempts to value options and other derivatives have a long history. One of the earliest endeavors to determine the value of stock options was made by Louis Bachelier in his Ph.D. thesis at the Sorbonne in 1900. The formula that he derived, however, was based on unrealistic assumptions, a zero interest rate, and a process that allowed for a negative share price.
Case Sprenkle, James Boness and Paul Samuelson improved on Bachelierís formula. They assumed that stock prices are log-normally distributed (which guarantees that share prices are positive) and allowed for a non-zero interest rate. They also assumed that investors are risk averse and demand a risk premium in addition to the risk-free interest rate. In 1964, Boness suggested a formula that came close to the Black-Scholes formula, but still relied on an unknown interest rate, which included compensation for the risk associated with the stock.
The attempts at valuation before 1973 basically determined the expected value of a stock option at expiration and then discounted its value back to the time of evaluation. Such an approach requires taking a stance on which risk premium to use in the discounting. This is because the value of an option depends on the risky path of the stock price, from the valuation date to maturity. But assigning a risk premium is not straightforward. The risk premium should reflect not only the risk for changes in the stock price, but also the investorsí attitude towards risk. And while the latter can be strictly defined in theory, it is hard or impossible to observe in reality.
The Black-Scholes formula
This yearís laureates resolved these problems by recognizing that it is not necessary to use any risk premium when valuing an option. This does not mean that the risk premium disappears, but that it is already incorporated in the stock price. In 1973 Fischer Black and Myron S. Scholes published the famous option pricing formula that now bears their name (Black and Scholes (1973)). They worked in close cooperation with Robert C. Merton, who, that same year, published an article which also included the formula and various extensions (Merton (1973)).
The idea behind the new method developed by Black, Merton and Scholes can be explained in the following simplified way. Consider a so-called European call option that gives the right to buy a certain share at a strike price of $100 in three months. (A European option gives the right to buy or sell only at a certain date, whereas a so-called American option gives the same right at any point in time up to a certain date.) Clearly, the value of this call option depends on the current share price; the higher the share price today the greater the probability that it will exceed $100 in three months, in which case it will pay to exercise the option. A formula for option valuation should thus determine exactly how the value of the option depends on the current share price. How much the value of the option is altered by a change in the current share price is called the “delta” of the option.
Assume that the value of the option increases by $1 when the current share price goes up $2 and decreases by $1 when the stock goes down $2 (i.e. delta is equal to one half). Assume also that an investor holds a portfolio of the underlying stock and wants to hedge against the risk of changes in the share price. He can then, in fact, construct a risk-free portfolio by selling (writing) twice as many options as the number of shares he owns. For reasonably small increases in the share price, the profit the investor makes on the shares will be the same as the loss he incurs on the options, and vice versa for decreases in the share price. As the portfolio thus constructed is risk free, it must yield exactly the same return as a risk-free three-month treasury bill. If it did not, arbitrage trading would begin to eliminate the possibility of making risk-free profits.
As the share price is altered over time and as the time to maturity draws nearer, the delta of the option changes. In order to maintain a risk-free stock-option portfolio, the investor has to change its composition. Black, Merton and Scholes assumed that such trading can take place continuously without any transaction costs (transaction costs were later introduced by others). The condition that the return on a risk-free stock-option portfolio yields the risk-free rate, at each point in time, implies a partial differential equation, the solution of which is the Black-Scholes formula for a call option:
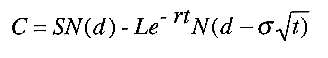 |
where the variable d is defined by:
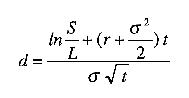
According to this formula, the value of the call option C , is given by the difference between the expected share price – the first term on the right-hand side – and the expected cost – the second term – if the option is exercised. The option value is higher, the higher the current share price S, the higher the volatility of the share price (as measured by its standard deviation) sigma, the higher the risk-free interest rate r, the longer the time to maturity t, the lower the strike price L, and the higher the probability that the option will be exercised (this probability is, under risk neutrality, evaluated by the standardized normal distribution function N ). All the parameters in the equation can be observed except sigma, which has to be estimated from market data. Alternatively, if the price of the call option is known, the formula can be used to solve for the marketís estimate of sigma.
The option pricing formula is named after Black and Scholes because they were the first to derive it. Black and Scholes originally based their result on the capital asset pricing model (CAPM, for which Sharpe was awarded the 1990 Prize). While working on their 1973 paper, they were strongly influenced by Merton. Black describes this in an article (Black (1989)):
“As we worked on the paper we had long discussions with Robert Merton, who also was working on option valuation. Merton made a number of suggestions that improved our paper. In particular, he pointed out that if you assume continuous trading in the option or the stock, you can maintain a relation between them that is literally riskless. In the final version of the paper we derived the formula that way because it seemed to be the most general derivation.”
It was thus Merton who devised the important generalization that market equilibrium is not necessary for option valuation; it is sufficient that there are no arbitrage opportunities. The method described in the example above is based precisely on the absence of arbitrage (and on stochastic calculus). It generalizes to valuation of other types of derivatives. Mertonís 1973 article also included the Black-Scholes formula and some generalizations; for instance, he allowed the interest rate to be stochastic. Four years later, he also developed (Merton (1977)) a more general method of deriving the formula which uses the fact that options can be created synthetically by trading in the underlying share and a risk-free bond.
Scientific importance
The option-pricing formula was the solution of a more than seventy-year old problem. As such, this is, of course, an important scientific achievement. The main importance of Black, Merton and Scholes´ contribution, however, refers to the theoretical and practical significance of their method of analysis. It has been highly influential in solving many economic problems. The scientific importance extends to both the pricing of derivative securities and to valuation in other areas.
Pricing of derivatives
The method described here has been enormously important for the pricing of derivative instruments. The laureates initiated the rapid evolution of option pricing that has taken place during the past two decades. Options on instruments other than shares give rise to other formulas that sometimes have to be solved numerically. The same method has been used to determine the value of currency options, interest rate options, options on futures, and so on.
Several of the original – and somewhat restrictive – assumptions behind the initial derivation of the Black-Scholes formula have subsequently been relaxed. In modern option pricing the interest rate can be stochastic, the volatility of the stock price can vary stochastically over time, the price process can include jumps, transaction costs can be positive, and the price process can be managed (e.g. as currencies are restricted to move inside bands). These extensions all rely on the method of analysis that Black, Merton and Scholes introduced.
Corporate liabilities
Black, Merton and Scholes realized already in 1973 that a share can be interpreted as an option on the whole firm (the title of their 1973 article is “The pricing of options and corporate liabilities”). When loans mature and the value of the firm is lower than the nominal value of debt, the shareholders have the right, but not the obligation, to repay the loans. The method can thus be used for determining the value of shares, which can be important if the shares are not traded. Since other corporate liabilities are also derivative instruments (whose value, too, depends on the value of the firm), they can be valued using the same method. Black, Merton and Scholes thus laid a satisfactory foundation for a unified theory to price all corporate liabilities.
Financial contract theory is undergoing rapid development. The Black-Merton-Scholes methodology has been important in recent efforts to design optimal financial contracts, taking into account various aspects of bankruptcy law.
Investment evaluation
In the choice between different investment alternatives, flexibility is a key factor. Machines may differ in their flexibility regarding the shut-down and start-up of production (as the market price of the product varies), the use of different sources of energy (as, say, the relative price between oil and electricity varies), etc. The Black-Merton-Scholes methodology can often be used to facilitate more informed investment decisions in such cases.
Guarantees and insurance contracts
Many types of insurance contracts and guarantees can be valued using modern option-pricing theory. Assume that an insurance company wants to determine the value of an insurance contract that protects a bondholder against the risk that the company issuing the bond will go bankrupt. The value of such an insurance contract can be approximated by a put option on the bond with a strike price equal to the nominal value of the bond. If the value of the bond declines below the strike price, the holder has the right to sell the bond at that price – that is, his possible loss is limited. In practice, therefore, an insurance company not only competes with other insurance companies, but also with the option market.
Complete markets
Methods developed by Merton (in Merton (1977)) have been used to extend the dynamic theory of financial markets. In the 1950s, Kenneth Arrow and Gerard Debreu (both previous laureates) showed how individuals or companies can eliminate their particular risk profile if there exist as many independent securities as there are future states of the world. This might well require a large number of securities. These findings have now been extended to show that a few financial instruments are sufficient to eliminate risk, even when the number of future states is very large.
Practical importance
The Chicago Board Options Exchange introduced trade in options in April 1973, one month before publication of the option-pricing formula. By 1975, traders on the options exchange had begun to apply the formula – using especially programmed calculators – to price and protect their option positions. Nowadays, thousands of traders and investors use the formula every day to value stock options in markets throughout the world.
Such rapid and widespread application of a theoretical result was new to economics. It was particularly remarkable since the mathematics used to derive the formula were not part of the standard training of practitioners or academic economists at that time.
The ability to use options and other derivatives to manage risks is quite valuable. For instance, portfolio managers use put options to reduce the risk of large declines in share prices. Companies use options and other derivative instruments to reduce risk. Banks and other financial institutions use the method developed by Black, Merton and Scholes to develop and determine the value of new products, sell tailor-made financial solutions to their customers, as well as to reduce their own risks by trading in financial markets.
Financial institutions employ mathematicians, economists and computer experts who have made important contributions to applied research in option theory. They have developed databases, new methods of estimating the parameters needed to value options and numerical methods to solve partial differential equations.
Some other scientific contributions
Merton and Scholes have made important scientific contributions in addition to those described so far.
Merton has made fundamental contributions (Merton (1969) and (1971)) to the analysis of individual consumption and investment decisions in continuous time. He presented (Merton (1973b)) an important generalization of CAPM, extending it from a static to a dynamic model. He also improved and generalized option pricing formula in different directions. In particular, he derived (Merton (1976)) a formula which allows stock price movements to be discontinuous.
Scholes has studied the effect of dividends on share prices (Black and Scholes (1974) and Miller and Scholes (1978) (1982)). He has also made empirical contributions, e.g. regarding estimation of b, the parameter that measures the risk of a share in the CAPM (Scholes and Williams (1977)), and market efficiency (Black, Jensen and Scholes (1972)).
Summary
Robert C. Merton and Myron S. Scholes have, in collaboration with the late Fischer Black, developed a pioneering formula for the valuation of stock options. Their method has had profound importance for economic valuations in many areas. It has also helped generate new financial instruments and facilitated more efficient management of risk in society.
References
Black, F. and Scholes, M., 1972, “The Valuation of Option Contracts and a Test of Market Efficiency”, Journal of Finance, Vol. 27, pp. 399-417.
Black, F. and Scholes, M., 1973, “The Pricing of Options and Corporate Liabilities”, Journal of Political Economy, Vol. 81, pp. 637-654.
Black, F. and Scholes, M., 1974, “The Effects of Dividend Yield and Dividend Policy on Common Stock Prices and Returns”, Journal of Financial Economics,Vol.1,pp.1-22.
Black, F., 1989, “How We Came Up with the Option Formula”, The Journal of Portfolio Management, Vol. 15, pp. 4-8.
Black F., Jensen, M.C. and Scholes, M., 1972, “The Capital Asset Pricing Model: Some Empirical Tests” in Jensen, M.C., ed., Studies in the Theory of Capital Markets, Praeger.
Merton, R.C., 1969, “Lifetime Portfolio Selection under Uncertainty: The Continuous-Time Case”, Review of Economics and Statistics, Vol. 51, pp. 247-257.
Merton, R.C., 1971, “Optimum Consumption and Portfolio Rules in a Continuous Time Model”, Journal of Economic Theory, Vol. 3, pp. 373-413.
Merton, R.C., 1973a, “Theory of Rational Option Pricing”, Bell Journal of Economics and Management Science, Vol. 4, pp. 637-654.
Merton, R.C., 1973b, “An Intertemporal Capital Asset Pricing Model”, Econometrica, Vol. 41, pp. 867-887.
Merton, R.C., 1976, “Option Pricing When Underlying Stock Returns Are Discontinuous”, Journal of Financial Economics, Vol. 3, pp. 125-144.
Merton, R.C., 1977, “On the Pricing of Contingent Claims and the Modigliani-Miller Theorem”, Journal of Financial Economics, Vol. 5, pp. 141-183.
Miller, M.H. and Scholes, M., 1978, “Dividends and Taxes”, Journal of Financial Economics, Vol. 6, pp. 333-364.
Miller, M.H. and Scholes, M., 1982, “Dividends and Taxes: Some Empirical Evidence”, Journal of Political Economy, Vol. 90, pp. 1118-1141.
Scholes, M. and Williams, J., 1977, “Estimating Betas from Nonsynchronous Data”, Journal of Financial Economics, Vol. 5, pp. 309-327.
Nobel Prizes and laureates
See them all presented here.
