Press release
English
Swedish

14 October 1997
The Royal Swedish Academy of Sciences has decided to award the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel, 1997, to
Professor Robert C. Merton, Harvard University, Cambridge, USA and
Professor Myron S. Scholes, Stanford University, Stanford, USA
for a new method to determine the value of derivatives.
Robert C. Merton and Myron S. Scholes have, in collaboration with the late Fischer Black, developed a pioneering formula for the valuation of stock options. Their methodology has paved the way for economic valuations in many areas. It has also generated new types of financial instruments and facilitated more efficient risk management in society.
***
In a modern market economy it is essential that firms and households are able to select an appropriate level of risk in their transactions. This takes place on financial markets which redistribute risks towards those agents who are willing and able to assume them. Markets for options and other so-called derivatives are important in the sense that agents who anticipate future revenues or payments can ensure a profit above a certain level or insure themselves against a loss above a certain level. (Due to their design, options allow for hedging against one-sided risk – options give the right, but not the obligation, to buy or sell a certain security in the future at a prespecified price.) A prerequisite for efficient management of risk, however, is that such instruments are correctly valued, or priced. A new method to determine the value of derivatives stands out among the foremost contributions to economic sciences over the last 25 years.
This year’s laureates, Robert Merton and Myron Scholes, developed this method in close collaboration with Fischer Black, who died in his mid-fifties in 1995. These three scholars worked on the same problem: option valuation. In 1973, Black and Scholes published what has come to be known as the Black-Scholes formula. Thousands of traders and investors now use this formula every day to value stock options in markets throughout the world. Robert Merton devised another method to derive the formula that turned out to have very wide applicability; he also generalized the formula in many directions.
Black, Merton and Scholes thus laid the foundation for the rapid growth of markets for derivatives in the last ten years. Their method has more general applicability, however, and has created new areas of research – inside as well as outside of financial economics. A similar method may be used to value insurance contracts and guarantees, or the flexibility of physical investment projects.
The problem
Attempts to value derivatives have a long history. As far back as 1900, the French mathematician Louis Bachelier reported one of the earliest attempts in his doctoral dissertation, although the formula he derived was flawed in several ways. Subsequent researchers handled the movements of stock prices and interest rates more successfully. But all of these attempts suffered from the same fundamental shortcoming: risk premia were not dealt with in a correct way.
The value of an option to buy or sell a share depends on the uncertain development of the share price to the date of maturity. It is therefore natural to suppose – as did earlier researchers – that valuation of an option requires taking a stance on which risk premium to use, in the same way as one has to determine which risk premium to use when calculating present values in the evaluation of a future physical investment project with uncertain returns. Assigning a risk premium is difficult, however, in that the correct risk premium depends on the investor’s attitude towards risk. Whereas the attitude towards risk can be strictly defined in theory, it is hard or impossible to observe in reality.
The method
Black, Merton and Scholes made a vital contribution by showing that it is in fact not necessary to use any risk premium when valuing an option. This does not mean that the risk premium disappears; instead it is already included in the stock price.
The idea behind their valuation method can be illustrated as follows:
Consider a so-called European call option that gives the right to buy one share in a certain firm at a strike price of $ 50, three months from now. The value of this option obviously depends not only on the strike price, but also on today’s stock price: the higher the stock price today, the greater the probability that it will exceed $ 50 in three months, in which case it pays to exercise the option. As a simple example, let us assume that if the stock price goes up by $ 2 today, the option goes up by $ 1. Assume also that an investor owns a number of shares in the firm in question and wants to lower the risk of changes in the stock price. He can actually eliminate that risk completely, by selling (writing) two options for every share that he owns. Since the portfolio thus created is risk-free, the capital he has invested must pay exactly the same return as the risk-free market interest rate on a three-month treasury bill. If this were not the case, arbitrage trading would begin to eliminate the possibility of making a risk-free profit. As the time to maturity approaches, however, and the stock price changes, the relation between the option price and the share price also changes. Therefore, to maintain a risk-free option-stock portfolio, the investor has to make gradual changes in its composition.
One can use this argument, along with some technical assumptions, to write down a partial differential equation. The solution to this equation is precisely the Black-Scholes’ formula. Valuation of other derivative securities proceeds along similar lines.
The Black-Scholes formula
Black and Scholes’ formula for a European call option can be written as
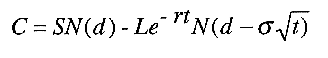
where the variable d is defined by
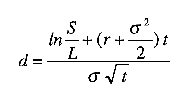 |
According to this formula, the value of the call option C, is given by the difference between the expected share value – the first term on the right-hand side – and the expected cost – the second term – if the option right is exercised at maturity. The formula says that the option value is higher the higher the share price today S, the higher the volatility of the share price (measured by its standard deviation) sigma, the higher the risk-free interest rate r, the longer the time to maturity t, the lower the strike price L, and the higher the probability that the option will be exercised (the probability is evaluated by the normal distribution function N ).
Other applications
Black, Merton and Scholes’ method has become indispensable in the analysis of many economic problems. Derivative securities constitute a special case of so-called contingent claims and the valuation method can often be used for this wider class of contracts. The value of the stock, preferred shares, loans, and other debt instruments in a firm depends on the overall value of the firm in essentially the same way as the value of a stock option depends on the price of the underlying stock. The laureates had already observed this in their articles published in 1973, thereby laying the foundation for a unified theory of the valuation of corporate liabilities.
A guarantee gives the right, but not the obligation, to exploit it under certain circumstances. Anyone who buys or is given a guarantee thus holds a kind of option. The same is true of an insurance contract. The method developed by this year’s laureates can therefore be used to value guarantees and insurance contracts. One can thus view insurance companies and the option market as competitors.
Investment decisions constitute another application. Many investments in equipment can be designed to allow more or less flexibility in their utilization. Examples include the ease with which one can close down and reopen production (in a mine, for instance, if the metal price is low) or the ease with which one can switch between different sources of energy (if, for instance, the relative price of oil and electricity changes). Flexibility can be viewed as an option. To choose the best investment, it is therefore essential to value flexibility in a correct way. The Black-Merton-Scholes’ methodology has made this feasible in many cases.
Banks and investment banks regularly use the laureates’ methodology to value new financial instruments and to offer instruments tailored to their customers’ specific risks. At the same time such institutions can reduce their own risk exposure in financial markets.
Other research contributions
Besides their valuation method, Merton and Scholes have made several significant contributions to financial economics. Merton has developed a new powerful method for analyzing consumption and investment decisions over time, and generalized the so-called CAPM (the valuation model for which William Sharpe was awarded the Prize in 1990) from a static to a dynamic setting. Scholes has clarified the impact of dividends on stock market values, together with Black and Miller (Merton Miller was awarded the Prize in 1990 for his contributions to corporate finance), and made empirical contributions, for example concerning estimation of the so-called beta value (a risk measure in the CAPM).
***
Further reading
Additional background material on the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel 1997
Black, F. och M. Scholes, 1973, “The Pricing of Options and Corporate Liabilities”, Journal of Political Economy, Vol. 81, pp. 637-654.
Black, F., 1989, “How We came Up with the Option Formula”, The Journal of Portfolio Management, Vol. 15, pp. 4-8
Hull, J.C., 1997, Options, Futures and Other Derivates, 3rd edition, Prentice Hall
Merton, R.C., 1973, “Theory of Rational Option Pricing”, Bell Journal of Economics and Management Science, Vol. 4, pp. 141-183.
***
Robert C. Merton, was born in 1944 in New York, USA. He received his Ph.D. in Economics in 1970 at MIT, Cambridge, USA. He currently holds the George Fisher Baker Professorship in Business Administration at Harvard Business School, Boston, USA.
Professor Robert C. Merton
Graduate School of Business Administration
Morgan Hall, Soldiers Field
Boston, MA 02163, USA
Myron S. Scholes, was born in 1941. He received his Ph.D. in 1969 at University of Chicago, USA. He currently holds the Frank E. Buck Professorship of Finance at the Graduate School of Business and is Senior Research Fellow at the Hoover Institution at Stanford University, Stanford, USA
Professor Myron S. Scholes
Graduate School of Business
Stanford University
Stanford, CA 94305, USA
Nobel Prizes and laureates
See them all presented here.
