Popular information

Information for the public:
Stable matching: Theory, evidence, and practical design (pdf)

Populärvetenskaplig information:
Stabil matchning: teori, evidens, och praktisk design (pdf)

The Prize in Economic Sciences 2012

This year’s Prize to Lloyd Shapley and Alvin Roth extends from abstract theory developed in the 1960s, over empirical work in the 1980s, to ongoing efforts to find practical solutions to real-world problems. Examples include the assignment of new doctors to hospitals, students to schools, and human organs for transplant to recipients. Lloyd Shapley made the early theoretical contributions, which were unexpectedly adopted two decades later when Alvin Roth investigated the market for U.S. doctors. His findings generated further analytical developments, as well as practical design of market institutions.

Stable matching: Theory, evidence, and practical design

Traditional economic analysis studies markets where prices adjust so that supply equals demand. Both theory and practice show that markets function well in many cases. But in some situations, the standard market mechanism encounters problems, and there are cases where prices cannot be used at all to allocate resources. For example, many schools and universities are prevented from charging tuition fees and, in the case of human organs for transplants, monetary payments are ruled out on ethical grounds. Yet, in these – and many other – cases, an allocation has to be made. How do such processes actually work, and when is the outcome efficient?

Matching theory

The Gale-Shapley algorithm

Analysis of allocation mechanisms relies on a rather abstract idea. If rational people – who know their best interests and behave accordingly – simply engage in unrestricted mutual trade, then the outcome should be efficient. If it is not, some individuals would devise new trades that made them better off. An allocation where no individuals perceive any gains from further trade is called stable. The notion of stability is a central concept in cooperative game theory, an abstract area of mathematical economics which seeks to determine how any constellation of rational individuals might cooperatively choose an allocation. The primary architect of this branch of game theory was Lloyd Shapley, who developed its main concepts in the 1950s and 1960s.

Unrestricted trading is a key presumption underlying the concept of stability. Although it allows clear analysis, it is difficult to imagine in many real-world situations. In 1962, Shapley applied the idea of stability to a special case. In a short paper, joint with David Gale, he examined the case of pairwise matching: how individuals can be paired up when they all have different views regarding who would be the best match.

Matching partners

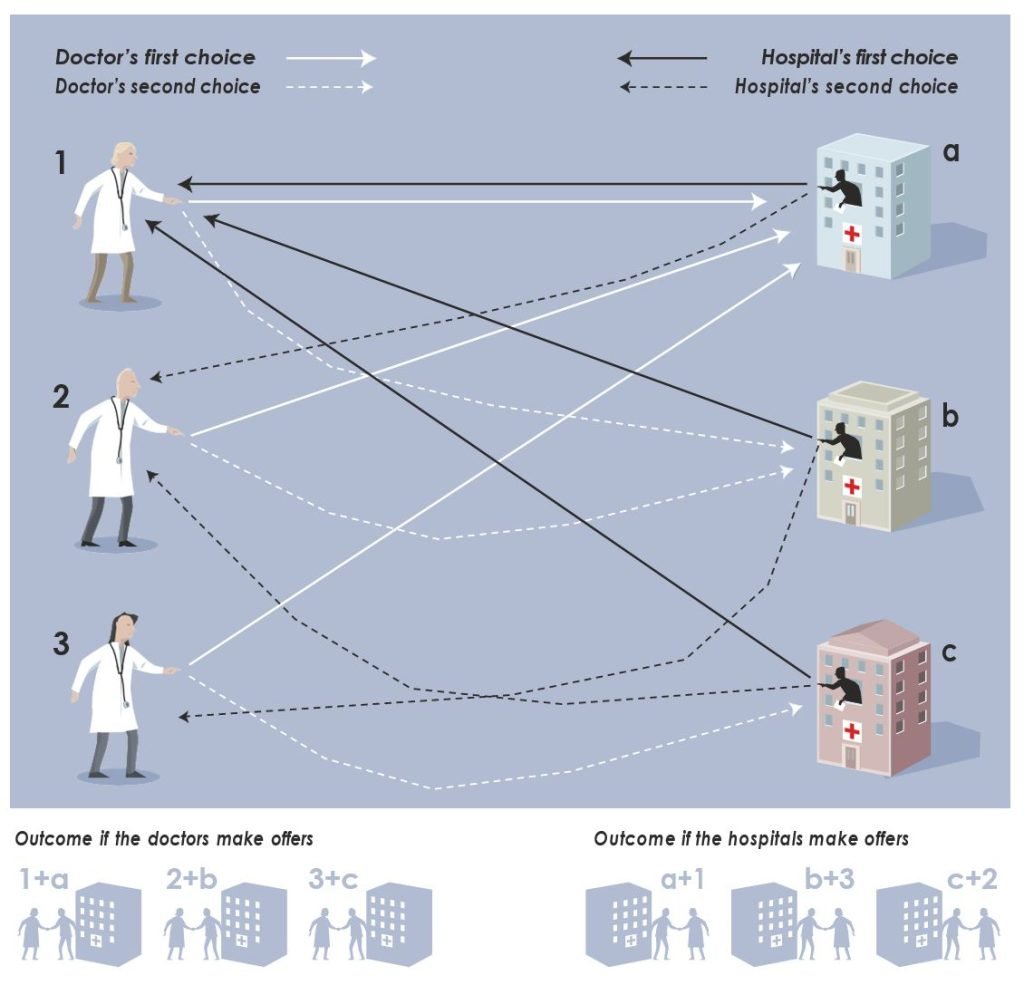
Gale and Shapley analyzed matching at an abstract, general level. They used marriage as one of their illustrative examples. How should ten women and ten men be matched, while respecting their individual preferences? The main challenge involved designing a simple mechanism that would lead to a stable matching, where no couples would break up and form new matches which would make them better off. The solution – the Gale-Shapley “deferred acceptance” algorithm – was a set of simple rules that always led straight to a stable matching.

The Gale-Shapley algorithm can be set up in two alternative ways: either men propose to women, or women propose to men. In the latter case, the process begins with each woman proposing to the man she likes the best. Each man then looks at the different proposals he has received (if any), retains what he regards as the most attractive proposal (but defers from accepting it) and rejects the others. The women who were rejected in the first round then propose to their second-best choices, while the men again keep their best offer and reject the rest. This continues until no women want to make any further proposals. As each of the men then accepts the proposal he holds, the process comes to an end. Gale and Shapley proved mathematically that this algorithm always leads to a stable matching.

The specific setup of the algorithm turned out to have important distributional consequences; it matters a great deal whether the right to propose is given to the women – as in our example – or to the men. If the women propose, the outcome is better for them than if the men propose, because some women wind up with men they like better, and no woman is worse off than if the men had been given the right to propose. Indeed, the resulting matching is better for the women than any other stable matching. Conversely, the reverse algorithm – where the men propose – leads to the worst outcome from the women’s perspective.

The clarity and elegance of the Gale-Shapley paper placed it on academic reading lists for economics students worldwide. But its real-world relevance was not recognized until much later. In the early 1980s, Alvin Roth set out to study a very practical allocation problem: the market for newly examined doctors.

Evidence

Markets for new doctors

In the U.S., students who graduate from medical school are typically employed as residents (interns) at hospitals, where they comprise a significant part of the labor force. In the early 1900s, this market was largely decentralized. During the 1940s, competition for scarce medical students forced hospitals to offer residencies (internships) increasingly early, sometimes several years before graduation. Matches were made before the students could produce evidence of their qualifications, and even before they knew which branch of medicine they would like to practice. When an offer was rejected, it was often too late to make offers to other candidates. A market ridden with such problems does not produce stable matches, because not enough offers can be made in time to ensure mutually beneficial trades. In order to make more offers quickly, hospitals imposed strict deadlines for responding to offers. This, in turn, forced students to make early decisions without knowing what other opportunities would become available later on.

In response to these problems, a centralized “clearinghouse”, called the National Resident Matching Program (NRMP), was introduced in the early 1950s. In a paper from 1984, Alvin Roth studied the algorithm used by this clearinghouse and discovered that it was closely related to the Gale-Shapley algorithm. He then hypothesized that the fundamental reason for the success of the NRMP was that it produced stable matches. In the early 1990s, Roth went on to study similar medical markets in the U.K. There, he found that different regions had adopted different algorithms, some of which produced stable matches and others not. Those which resulted in stable matches had turned out to be successful, whereas the other algorithms had broken down in various ways.

Practical design

Matching doctors and hospitals

Despite its success, the NRMP still encountered problems. The number of female medical students had grown, and it became increasingly common that dual-doctor couples looked for internships in the same region. The NRMP could not accommodate these requests, so that many applicants chose not to use the mechanism: a sign that it was not stable. The NRMP – where the hospitals offered positions to students – was also criticized for systematically favoring hospitals over students. Indeed, as Gale and Shapley had shown theoretically, the proposing side of the market (in this case, the hospitals) is systematically favored. In 1995, Roth was asked to help design an improved algorithm that would eliminate these problems. Along with Elliott Peranson, he formulated an algorithm, built on applicant proposals and designed to accommodate couples. The new algorithm, adopted by the NRMP in 1997, has worked well and over 20,000 positions per year have since been matched with applicants.

The research underlying the revised design prompted the development of new theory. It seemed that applicants could manipulate the original algorithm – by turning down offers which they actually preferred and keeping those which were worse – in order to achieve a better outcome. In several theoretical papers, Roth showed how misrepresentation of one’s true preferences might be in the interest of the receiving side (students in the original NRMP) in some algorithms. Drawing on this insight, the revised NRMP algorithm was designed to be immune to student misrepresentation. Furthermore, computer simulations verified that, in practice, it was not sensitive to strategic manipulation by the hospitals.

Matching students and high-schools

The Gale-Shapley algorithm proved to be useful in other applications, such as high-school choice. Up until 2003, applicants to New York City public high schools were asked to rank their five most preferred choices, after which these preference lists were sent to the schools. The schools then decided which students to admit, reject, or place on waiting lists. The process was repeated in two more rounds, and students who had not been assigned to any school after the third round were allocated through an administrative process. However, this did not provide the applicants with enough oppor- tunities to list their preferences, and the schools did not have enough opportunities to make offers. As a result, about 30,000 students per year ended up at schools they had not listed. Moreover, the process gave rise to misrepresentation of preferences. Since schools were more likely to admit students who ranked them as their first choice, students unlikely to be admitted to their favorite school found it in their best interest to list a more realistic option as their first choice, while applicants who simply reported their true preferences suffered unnecessarily poor outcomes. In 2003, Roth and his colleagues helped redesign this admissions process, based on an applicant-proposing version of the Gale-Shapley algorithm. The new algorithm proved to be successful, with a 90 percent reduction in the number of students assigned to schools for which they had expressed no preference. Today, a growing number of U.S. metropolitan areas use some variant of the Gale-Shapley algorithm.

Matching kidneys and patients

The matching settings described so far involve two sides that both make active decisions. Some real-world situations are one-sided, however, in the sense that the other side is entirely passive. A practical example is the matching of kidneys and other human organs to patients in need of a transplant. How can this be accomplished in an efficient way?

This problem was studied by Shapley and his colleagues, again in the abstract and based on the notion of stability. The proposed algorithm – the so-called top trading cycle – is in fact very simple. It is based on an initial allocation of objects and subsequent swapping. A challenge in the case of human organs is that some kidney-patient pairs may not be compatible and that complex multilateral swaps may be quite time consuming. Again, a combination of theory and experimental work has been used to compare different versions of top trading. As a result, increasingly complex chains of kidney donations are now adopted in a number of U.S. states.

Extensions to new markets

A striking feature of the above examples is that prices are not part of the process. Does the absence of a price mechanism in the basic Gale-Shapley algorithm limit its applicability? Not necessarily. Shapley and others examined extensions of the original model that allow for prices (salaries, in the market for doctors) to be part of the offers. Algorithms including prices work in much the same way and produce stable matches with broadly similar features. In fact, matching with prices is closely related to auctions, where objects are matched with buyers and where prices are decisive. Research that relates matching algorithms to auctions has recently generated interesting theoretical results, which appear to be applicable in practice. A case in point is the internet auction, in particular search engines that auction out space for advertisers. Companies in this business have benefited from insights inherent in the Gale-Shapley algorithms and have used top economists as experts in designing new auctions.

This year’s prize rewards a flourishing field of research, where theory, evidence, and design are used interactively. Lloyd Shapley and Alvin Roth have worked independently of each other, but the success of their research is due to the combination of Shapley’s theoretical results with Roth’s insights into their practical value. The field continues to grow and holds great promise for the future.

Links and further reading

Blog

Market Design
www.marketdesigner.blogspot.se

Lectures (video)

Roth, A. E. (2007) What Have We Learned from Market Design, Rosenthal Memorial Lecture. Boston University.
www.youtube.com/watch?v=7qrYC0Ojf-o

Roth, A. E. (2007) Market Failure and Market Design, Google Tech Talks.
www.youtube.com/watch?v=4tdOY-HHC7s

Review article

Roth A. E. (2008) What have we learned from market design?, Economic Journal, 118: 285–310.

Books

Moulin H. (1995) Cooperative Microeconomics. Princeton University Press.

Roth A. E. and Sotomayor M. (1990) Two-sided Matching: a Study in Game-theoretic Modeling and Analysis, Econometric Society Monograph Series, Cambridge University Press.

Scientific articles

Gale, D. and L. S. Shapley (1962) College admissions and the stability of marriage, American Mathematical Monthly, 69: 9–15.

Serrano, R. (2009) Cooperative games: core and Shapley value, In: Encyclopedia of Complexity and Systems Science, Edited by R. Meyers. New York: Springer.

The Laureates

ALVIN E. ROTH
U.S. citizen. Born 1951 in USA. Ph.D. 1974 from Stanford University, Stanford, CA, USA. George Gund Professor of Economics and Business Administration at Harvard University, Cambridge, MA, USA, and Harvard Business School, Boston, MA, USA.
http://kuznets.fas.harvard.edu/~aroth/alroth.html

LLOYD S. SHAPLEY
U.S. citizen. Born 1923 in Cambridge, MA, USA. Ph.D. 1953 from Princeton University, Princeton, NJ, USA. Professor Emeritus at University of California, Los Angeles, CA, USA.
www.econ.ucla.edu/shapley/index.html