Popular information
Popular science background:
Strange phenomena in matter’s flatlands (pdf)
Populärvetenskaplig information:
Märkliga företeelser i materiens plattland (pdf)

The Nobel Prize in Physics 2015
This year’s Laureates opened the door on an unknown world where matter exists in strange states. The Nobel Prize in Physics 2016 is awarded with one half to David J. Thouless, University of Washington, Seattle, and the other half to F. Duncan M. Haldane, Princeton University, and J. Michael Kosterlitz, Brown Univer- sity, Providence. Their discoveries have brought about breakthroughs in the theoretical understanding of matter’s mysteries and created new perspectives on the development of innovative materials.
Strange phenomena in matter’s flatlands
David Thouless, Duncan Haldane, and Michael Kosterlitz have used advanced mathematical methods to explain strange phenomena in unusual phases (or states) of matter, such as superconductors, superfluids or thin magnetic films. Kosterlitz and Thouless have studied phenomena that arise in a flat world – on surfaces or inside extremely thin layers that can be considered two-dimensional, compared to the three dimensions (length, width and height) with which reality is usually described. Haldane has also studied matter that forms threads so thin they can be considered one-dimensional.
The physics that takes place in the flatlands is very different to that we recognise in the world around us. Even if very thinly distributed matter consists of millions of atoms, and even if each atom’s behaviour can be explained using quantum physics, atoms display completely different properties when lots of them come together. New collective phenomena are being continually discovered in these flatlands, and condensed matter physics is now one of the most vibrant fields in physics.
The three Laureates’ use of topological concepts in physics was decisive for their discoveries. Topology is a branch of mathematics that describes properties that change step-wise. With modern topology as a tool, this year’s Laureates presented surprising results, which have opened up new fields of research and led to the creation of new and important concepts within several areas of physics.
Quantum physics becomes visible in the cold
Deep down, all matter is governed by the laws of quantum physics. Gases, liquids and solids are the usual phases of matter, in which quantum effects are often hidden by random atomic movements. But in extreme cold, close to absolute zero (–273 degrees Celsius) matter assumes strange new phases and behaves in unexpected ways. Quantum physics, which otherwise only works in the micro-scale world, suddenly becomes visible (fig. 1).
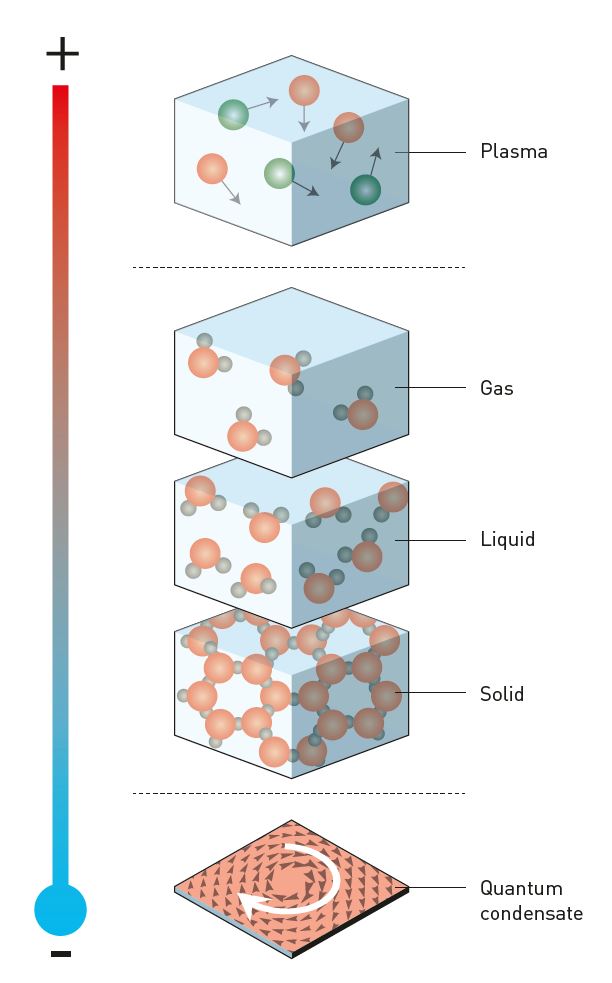
Ordinary phases of matter also transition between each other when the temperature changes. For example, such a phase transition occurs when ice, which consists of well-ordered crystals, is heated and melts into water, a more chaotic phase of matter. When we look at matter’s little known flatlands, we find material phases that have not yet been fully explored.
Strange things can happen in the cold. For example, the resistance otherwise encountered by all moving particles suddenly ceases. This is the case when electrical current flows with no resistance in a superconductor, or when a vortex in a superfluid spins forever without slowing down.
The first person to systematically study superfluids was the Russian Pyotr Kapitsa, in the 1930s. He cooled helium-4, which is found in air, to –271 degrees Celsius and made it crawl up the sides of its holder. In other words, it behaved just as strangely as a superfluid should when viscosity has completely vanished. Kapitsa was rewarded with the 1978 Nobel Prize in Physics, and since then several types of superfluids have been created in the laboratory. Superfluid helium, thin films of superconductors, thin layers of magnetic materials and electrically conductive nanothreads are a few of the many new material phases that are now being intensively studied.
Vortex pairs provided the solution
Researchers long believed that thermal fluctuations destroy all order in matter in a flat, two-dimensional world, even at absolute zero. If there are no ordered phases, there can be no phase transitions. But in the early 1970s, David Thouless and Michael Kosterlitz met in Birmingham, Great Britain, and they challenged the then current theory. Together, they took on the problem of phase transitions in the flatlands (the former out of curiosity, the latter out of ignorance, they themselves claim). This cooperation resulted in an entirely new understanding of phase transitions, which is regarded as one of the twentieth century’s most important discoveries in the theory of condensed matter physics. It is called the KT transition (Kosterlitz-Thouless transition) or the BKT transition, where the B is for Vadim Berezinskii, a now deceased theoretical physicist from Moscow who had presented similar ideas.
The topological phase transition is not an ordinary phase transition, like that between ice and water. The leading role in a topological transition is played by small vortices in the flat material. At low temperatures they form tight pairs. When the temperature rises, a phase transition takes place: the vortices suddenly move away from each other and sail off in the material on their own (fig. 2).
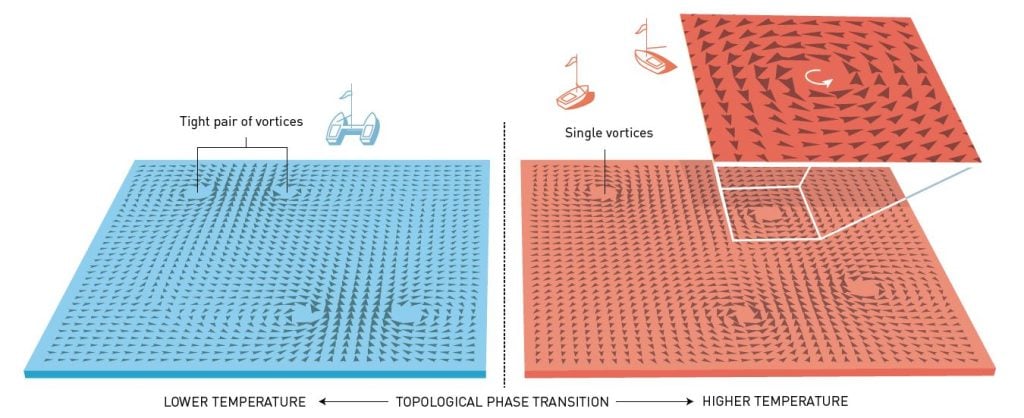
The wonderful thing about this theory is that it can be used for different types of materials in low dimensions – the KT transition is universal. It has become a useful tool, one that is not only applied in the world of condensed matter, but also in other areas of physics, such as atomic physics or statistical mechanics. The theory behind the KT transition has also been developed by both its originators and others, and also confirmed experimentally.
The mysterious quantum leaps
Experimental developments eventually brought about a number of new states of matter that required explanation. In the 1980s, both David Thouless and Duncan Haldane presented groundbreaking new theoretical work that challenged previous theories, of which one was the quantum mechanical theory for determining which materials conduct electricity. This had initially been developed in the 1930s and, a few decades later, this area of physics was considered to be well understood.
It was therefore a great surprise when, in 1983, David Thouless proved that the previous picture was incomplete and, at low temperatures and in strong magnetic fields, a new type of theory was necessary, one where topological concepts were vital. At around the same time, Duncan Haldane also arrived at a similar, and similarly unexpected, conclusion while analysing magnetic atomic chains. Their work has been instrumental in the subsequent dramatic developments to the theory of new phases of matter.
The mysterious phenomenon that David Thouless described theoretically, using topology, is the quantum Hall effect. This was discovered in 1980 by the German physicist Klaus von Klitzing, who was rewarded with the Nobel Prize in 1985. He studied a thin conducting layer between two semiconductors, where the electrons were cooled to a few degrees above absolute zero and subjected to a strong magnetic field.
In physics, it is not uncommon for drastic things to happen when the temperature is lowered; for example, many materials become magnetic. This happens because all the small atomic magnets in the material suddenly point in the same direction, giving rise to a strong magnetic field, which can also be measured.
However, the quantum Hall effect is more difficult to understand; the electrical conductance in the layer appears to only be able to assume particular values, which are also extremely precise, something that is unusual in physics. Measurements provide precisely the same results even if the temperature, magnetic field or the amount of impurities in the semiconductor vary. When the magnetic field changes enough, the conductance of the layer also changes, but only in steps; reducing the strength of the magnetic field makes electrical conductance first exactly twice as big, then it triples, quadruples, and so on. These integer steps could not be explained by the physics known at the time, but David Thouless found the solution to this riddle using topology.
Answered by topology
Topology describes the properties that remain intact when an object is stretched, twisted or deformed, but not if it is torn apart. Topologically, a sphere and a bowl belong to the same category, because a spherical lump of clay can be transformed into a bowl. However, a bagel with a hole in the middle and a coffee cup with a hole in the handle belong to another category; they can also be remodelled to form each other’s shapes. Topological objects can thus contain one hole, or two, or three, or four … but this number has to be an integer. This turned out to be useful in describing the electrical conductance found in the quantum Hall effect, which only changes in steps that are exact multiples of an integer (fig. 3).
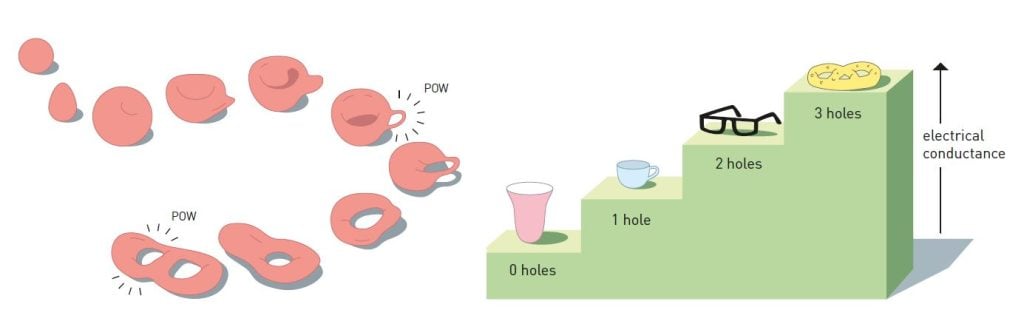
In the quantum Hall effect, electrons move relatively freely in the layer between the semi-conductors and form something called a topological quantum fluid. In the same way as new properties often appear when many particles come together, electrons in the topological quantum fluid also display surprising characteristics. Just as it can’t be ascertained whether there is a hole in a coffee cup by only looking at a small part of it, it is impossible to determine whether electrons have formed a topological quantum fluid if you only observe what is happening to some of them. However, conductance describes the electrons’ collective motion and, because of topology, it varies in steps; it is quantised. Another characteristic of the topological quantum fluid is that its borders have unusual properties. These were predicted by the theory and were later confirmed experimentally.
Another milestone occurred in 1988, when Duncan Haldane discovered that topological quantum fluids, like the one in the quantum Hall effect, can form in thin semiconductor layers even when there is no magnetic field. He said he’d never dreamed of his theoretical model being realised experimentally but, as recently as 2014, this model was validated in an experiment using atoms that were cooled to almost absolute zero.
New topological materials in the pipeline
In much earlier work, from 1982, Duncan Haldane made a prediction that amazed even the experts in the field. In theoretical studies of chains of magnetic atoms that occur in some materials, he discovered that the chains had fundamentally different properties depending on the character of the atomic magnets. In quantum physics there are two types of atomic magnets, odd and even. Haldane demonstrated that a chain formed of even magnets is topological, while a chain of odd magnets is not. Like the topological quantum fluid, it is not possible to determine whether an atomic chain is topological or not by simply investigating a small part of it. And, just as in the case of the quantum fluid, the topological properties reveal themselves at the edges. Here, this is at the ends of the chain, because the quantum property known as spin halves at the ends of a topological chain.
Initially, no one believed Haldane’s reasoning about atomic chains; researchers were convinced that they already completely understood them. But it turned out that Haldane had discovered the first example of a new type of topological material, which is now a lively field of research in condensed matter physics.
Both quantum Hall fluids and even magnetic atomic chains are included in this new group of topological states. Later, researchers discovered several other unexpected topological states of matter, not only in chains and thin border layers, but also in ordinary three-dimensional materials.
Topological insulators, topological superconductors and topological metals are now being talked about. These are examples of areas which, over the last decade, have defined frontline research in condensed matter physics, not least because of the hope that topological materials will be useful for new generations of electronics and superconductors, or in future quantum computers. Current research is now revealing the secrets of matter in the exotic flatlands discovered by this year’s Nobel Laureates.
The Royal Swedish Academy of Sciences has decided to award the Nobel Prize in Physics 2016
with one half to
DAVID J. THOULESS
Born 1934 in Bearsden, UK. Ph.D. 1958 from Cornell University, Ithaca, NY, USA. Emeritus Professor at University of Washington, Seattle, WA, USA.
https://sharepoint.washington.edu/ phys/people/Pages/view-person. aspx?pid=85
and the other half to
F. DUNCAN M. HALDANE
Born 1951 in London, UK. Ph.D. 1978 from Cambridge University, UK. Eugene Higgins Professor of Physics at Princeton University, NJ, USA.
www.princeton.edu/physics/people/display_person.xml?netid=haldane&di splay=faculty
and
J. MICHAEL KOSTERLITZ
Born 1942 in Aberdeen, UK. Ph.D. 1969 from Oxford University, UK. Harrison E. Farnsworth Professor of Physics at Brown University, Providence, RI, USA.
https://vivo.brown.edu/display/jkosterl
”for theoretical discoveries of topological phase transitions and topological phases of matter”
Science Editors: Thors Hans Hansson, David Haviland and Gunnar Ingelman, the Nobel Committee for Physics
Text: Joanna Rose
Translation: Clare Barnes
Illustrations: © Johan Jarnestad/The Royal Swedish Academy of Sciences
Editor: Fredrik All
© The Royal Swedish Academy of Sciences
Nobel Prizes and laureates
Six prizes were awarded for achievements that have conferred the greatest benefit to humankind. The 12 laureates' work and discoveries range from proteins' structures and machine learning to fighting for a world free of nuclear weapons.
See them all presented here.
