Press release
English
Swedish

13 October 1998
The Royal Swedish Academy of Sciences has awarded the 1998 Nobel Prize in Physics jointly to
Professor Robert B. Laughlin, Stanford University, California, USA,
Professor Horst L. Störmer, Columbia University, New York and Lucent Technologies’ Bell Labs, New Jersey, USA, and
Professor Daniel C. Tsui, Princeton University, Princeton, New Jersey, USA.
The three researchers are being awarded the Nobel Prize for discovering that electrons acting together in strong magnetic fields can form new types of “particles”, with charges that are fractions of electron charges.
Citation:
“for their discovery of a new form of quantum fluid with fractionally charged excitations.”
Electrons in New Guises
Horst L. Störmer and Daniel C. Tsui made the discovery in 1982 in an experiment using extremely powerful magnetic fields and low temperatures. Within a year of the discovery Robert B. Laughlin had succeeded in explaining their result. Through theoretical analysis he showed that the electrons in a powerful magnetic field can condense to form a kind of quantum fluid related to the quantum fluids that occur in superconductivity and in liquid helium. What makes these fluids particularly important for researchers is that events in a drop of quantum fluid can afford more profound insights into the general inner structure and dynamics of matter. The contributions of the three laureates have thus led to yet another breakthrough in our understanding of quantum physics and to the development of new theoretical concepts of significance in many branches of modern physics.
Quantum effects become visible
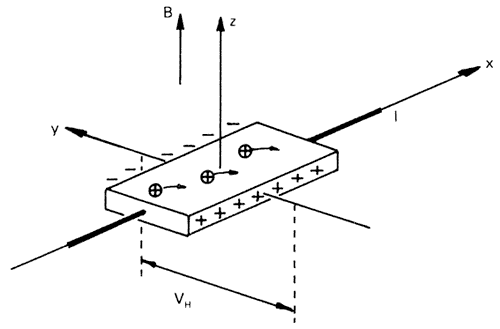
As a young student in 1879 Edwin H. Hall discovered an unexpected phenomenon. He found that if a thin gold plate is placed in a magnetic field at right angles to its surface an electric current flowing along the plate can cause a potential drop at right angles both to the current and the magnetic field (see figure 1). Termed the Hall effect, this takes place because electrically charged particles (in this case electrons) moving in a magnetic field are influenced by a force and deflect laterally. The Hall effect can be used to determine the density of charge carriers (negative electrons or positive holes) in conductors and semi-conductors, and has become a standard tool in physics laboratories the world over.
 |
|
Fig. 1. A voltage V drives a current I in the positive x direction. Normal Ohmic resistance is V / I. A magnetic field in the positive z direction shifts positive charge carriers in the negative y direction. This generates a Hall potential ( VH) and a Hall resistance (VH/ I ) in the y direction. (Kosmos 1986) |
Hall performed his experiments at room temperature and with moderate magnetic fields of less than one tesla (T). At the end of the 1970’s researchers used extremely low temperatures (only a few degrees from absolute zero, i.e. around -272°C) and very powerful magnetic fields (max approx. 30 T). They studied the Hall effect in the type of semiconductor design used in the electronics industry for manufacturing low-noise transistors. The material contains electrons which, though trapped close to an internal surface, separating two distinct parts of the material, are highly mobile along the surface.
In such a layer at low temperatures electrons can be caused to move as if on a plane surface, i.e. in two dimensions only. This geometrical limitation leads to many unexpected effects. One is that the Hall effect changes character. This is seen most simply when one measures how the Hall resistance varies with the strength of the applied magnetic field.
In 1980 the German physicist Klaus von Klitzing discovered in a similar experiment that the Hall resistance does not vary in linear fashion, but “stepwise” with the strength of the magnetic field (see figure 2). The steps occur at resistance values that do not depend on the properties of the material but are given by a combination of fundamental physical constants divided by an integer. We say that the resistance is quantized. At quantized Hall resistance values, normal Ohmic resistance disappears and the material becomes in a sense superconducting.
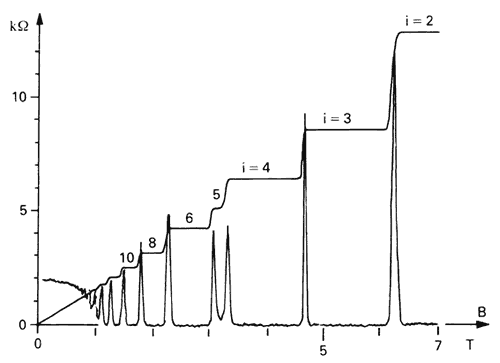
Fig. 2. The Hall resistance varies stepwise with changes in magnetic field B. Step height is given by the physical constant h/e2 ( value approximately 25 kilo-ohm ) divided by an integer i. The figure shows steps for i =2,3,4,5,6,8 and 10. The effect has given rise to a new international standard for resistance. Since 1990 this has been represented by the unit 1 klitzing, defined as the Hall resistance at the fourth step ( h/4e2 ). The lower peaked curve represents the Ohmic resistance, which disappears at each step. (Kosmos 1986)
For his discovery of what is termed the integer quantum Hall effect von Klitzing received the Nobel Prize in Physics in 1985. The effect may be understood if one accepts the laws of quantum physics for how individual electrons behave in powerful magnetic fields. In simple terms, the electrons move only in certain circular paths, the basic sizes of which are determined by the magnetic field. The various steps turn out to show how many of the smallest paths are entirely full of electrons.
In their refined experimental studies of the quantum Hall effect, using among other things lower temperatures and more powerful magnetic fields, Störmer, Tsui and their co-workers found to their great surprise a new step in the Hall resistance which was three times higher than von Klitzing’s highest. They subsequently found more and more new steps, both above and between the integers. All the new step heights can be expressed with the same constant as earlier but now divided by different fractions. For this reason the new discovery was named the fractional quantum Hall effect. It posed a great mystery for the researchers who could not explain how the new steps came about.
A new type of quantum fluid
A year after the discovery of the fractional quantum Hall effect, Laughlin offered a theoretical explanation. According to his theory the low temperature and the powerful magnetic field compel the electron gas to condense to form a new type of quantum fluid. Since electrons are most reluctant to condense (they are what is termed fermions) they first, in a sense, combine with the “flux quanta” of the magnetic field. Particularly for the first steps discovered by Störmer and Tsui, the electrons each capture three flux quanta, thus forming a kind of composite particle with no objection to condensing (they become what is termed bosons).
Quantum fluids have earlier occurred at very low temperatures in liquid helium (1962 Nobel Prize to Landau; 1978 to Kapitsa; 1996 to Lee, Osheroff and Richardson) and in superconductors (1913 Nobel prize to Kamerlingh Onnes; 1972 to Bardeen, Cooper and Schrieffer; 1987 to Bednorz and Müller). Quantum fluids have certain properties in common, e.g. superfluidity, but they also show important differences in behaviour. Some, like Laughlin’s fluid, consist of composite particles.
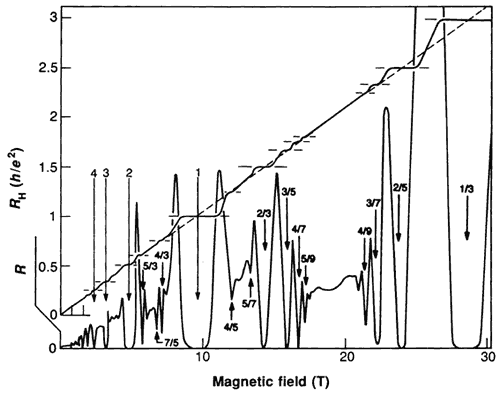
Apart from its superfluidity, which explains the disappearance of Ohmic resistance at the Hall resistance steps, the new quantum fluid proposed by Laughlin has many unusual properties. One of the most remarkable is that if one electron is added the fluid will be affected (excited) and a number of fractionally charged “quasiparticles” created. These quasiparticles are not particles in the normal sense but a result of the common dance of electrons in the quantum fluid. Laughlin was the first to demonstrate that the quasiparticles have precisely the correct fractional charge to explain Störmer’s and Tsui’s results. Subsequent measurements have demonstrated more and more fractionally charged steps in the Hall effect (see figure 3), and Laughlin’s quantum fluid has proved capable of explaining all the steps found experimentally.
 |
|
Fig. 3. The dashed diagonal line represents the classical Hall resistance and the full drawn diagonal stepped curve the experimental results. The magnetic fields causing the steps are marked with arrows. Note particularly the step first discovered by Störmer and Tsui (1/3) at the highest value of the magnetic field and the steps earlier discovered by von Klitzing (integers) with a weaker magnetic field. (Science 1990) |
The new quantum fluid strongly resists compression; it is said to be incompressible. This is because it reacts to compression by forming more quasiparticles, which costs energy.
Direct demonstration of quasiparticles
The discovery and the explanation of the fractional quantum Hall effect in 1982-83 may be said to represent an indirect demonstration of the new quantum fluid and its fractionally charged quasiparticles. Several research groups have recently succeeded in observing these new particles directly (see reference list). This has for instance taken place in experiments where very small variations in a current have been ascribable to individual quasiparticles flowing through the circuit. These measurements, comparable to distinguishing the sound of individual hailstones during a hailstorm and determining that they are only a fraction of their normal size, were made possible by the astonishing development of microelectronics since this year’s three laureates made their pioneering contributions. The measurements may be viewed as the conclusive verification of their discoveries.
| Further reading |
| Additional background material on the Nobel Prize in Physics 1998 [pdf] |
| Splitting the electron, by B. Daviss, New Scientist, 31 January 1998, p. 36. |
| Fractionally charged quasiparticles signal their presence with noise, by G. P. Collins, Physics Today, November 1997, p. 17. |
| When the electron falls apart, by P.W. Anderson, Physics Today, October 1997, p. 42. |
| Electrons in flatland, by S. Kivelson, D.H. Lee and S.C. Zhang, Scientific American, March 1996, p.64. |
| Composite Fermions: New particles in the fractional quantum Hall effect, by H. Störmer and D. Tsui, Physics News in 1994, American Institute of Physics 1995, p. 33. |
| The fractional quantum Hall effect, by J.P. Eisenstein and H.L. Stormer, Science, 22 June 1990, p. 1510. |
Robert B. Laughlin
born 1950 in Visalia, CA, USA. American citizen. PhD in physics 1979 at Massachusetts Institute of Technology, Cambridge, USA. Professor of Physics at Stanford University since 1989. Laughlin has received among other awards the 1986 Oliver E. Buckley Prize from the American Physical Society and the Medal of the Franklin Institute, 1998, for his work associated with the fractional quantum Hall effect.
Professor Robert B. Laughlin
Department of Physics, Varian Bldg
Stanford University
Stanford, CA 94305-4060
USA
Horst L. Störmer
born 1949 in Frankfurt/Main. PhD in physics 1977 at Stuttgart University, Germany. Director of Physical Research Laboratory, Bell Laboratories 1992-97. Professor, Columbia University, New York and Adjunct Physics Director at Lucent Technologies’ Bell Labs since 1998. Störmer received among other awards the 1984 Oliver E. Buckley Prize from the American Physical Society, and the Medal of the Franklin Institute, 1998, for his work associated with the fractional quantum Hall effect.
Professor Horst L. Störmer
Physics Department
Columbia University
New York, NY 10027
USA
Daniel C. Tsui
born 1939 in Henan, China. American citizen. PhD in physics 1967 at University of Chicago, USA. Professor at Princeton University since 1982. Tsui received among other awards the 1984 Oliver E. Buckley Prize from the American Physical Society, and the Medal of the Franklin Institute, 1998, for his work associated with the fractional quantum Hall effect.
Professor Daniel C. Tsui
Department of Electrical Engineering
Princeton University
PO Box 5263
Princeton, NJ 08544
USA
Nobel Prizes and laureates
See them all presented here.
