Information for the public:
Asymmetric information and economic institutions (pdf)

Populärvetenskaplig information:
Asymmetrisk information och ekonomiska institutioner (pdf)

The Prize in Economic Sciences 2007

Buyers and sellers sometimes haggle too hard and therefore fail to trade. Desirable joint projects are sometimes not undertaken because the projects’ beneficiaries fail to agree how the costs should be shared. Sickness insurance, for example, is typically criticized either for offering too little coverage or for inviting misuse. In either case, the basic problem is that people have an incentive to economize with their private information: some insurancy-policy sellers claim that their costs are high in order to increase the price; some beneficiaries of joint projects such as insurance-policy holders claim that their benefits are low in order to reduce their own contributions to the project; some well-insured workers claim that they are sick, in order to reduce their workload.

Asymmetric information and economic institutions

An important goal of economic theory is to understand what institutions, or allocation mechanisms, are best suited to minimize the economic losses generated by private information. What trading mechanisms will realize the largest gains from trade, and what mechanisms will maximize the seller’s expected revenue? What collective decision-making procedures will succeed in implementing desirable joint projects while denying funds for undesirable projects? What insurance schemes will provide the best coverage without inviting misuse?

Mechanism design theory, initiated by Leonid Hurwicz and refined and applied by Eric Maskin and Roger Myerson, provides tools for analyzing and answering and these questions and many others like them. For example, mechanism design theory shows why an auction is typically the most efficient institution for the allocation of private goods¹ among a given set of potential buyers, and it frequently also specifies what auction format will give the largest expected revenue for the seller. Likewise, mechanism design theory explains why there is often no good market solution to the problem of providing public goods.² Indeed, the theory demonstrates why the efficient provision of public goods may require substantial departures from the principles of unanimous decision-making.

Before the advent of mechanism design, microeconomic analysis of resource allocation mechanisms was very largely a theory of markets. A central question was: When will a market mechanism suffice to allocate resources efficiently? It could be shown that the market implements fully efficient outcomes under very stringent (unrealistic) conditions such as perfect competition, freely available information, private goods, and the absence of any environmental effects of production and consumption. Mechanism design theory asks a much more general question: What resource allocation mechanism produces the best attainable outcome under more general conditions? One part of the answer is that markets, even if they do not attain full efficiency, perform at least as well as any other mechanism under conditions that are considerably less stringent than the conditions for full efficiency. For example, so-called double auctions – where buyers as well as sellers submit bids – are frequently unbeaten mechanisms for trading private goods. Another part of the answer is that markets can be ill suited for providing public goods. The funding of such joint projects may require another institutional framework, admitting for example, taxation of potential users.

While it has long been understood that markets could still be desirable even when they are not perfect, and that public goods may sometimes justify funding through taxation, mechanism design theory made these intuitions much more precise. It provides a tool for characterizing the optimal institution for any given set of conditions, thereby enabling a much deeper scientific analysis of the merits of alternative institutions. Applications of mechanism design theory have thus led to major breakthroughs in many areas of economics, including regulation theory, corporate finance, the theory of taxation, and voting procedures.

Key concepts and results

The development of mechanism design theory originated with the work of Leonid Hurwicz (1960). He defined a mechanism as a game in which the participants send messages to each other and/or to a “message center”, and where a pre-specified rule assigns an outcome (such as an allocation of goods and services) to every collection of received messages. For given assumptions about participants’ preferences and beliefs, each rule induces one or more predicted outcomes – or equilibria. Within this framework, the predicted outcomes associated with markets and market-like institutions can be compared with the predicted outcomes of a vast array of alternative trading institutions. Hurwicz (1972) also introduced the key notion of incentive compatibility, which proved central to later developments.

In the 1970s, the formulation of the so-called revelation principle and the development of implementation theory led to great advances in the theory of mechanism design. The revelation principle is an insight that greatly simplifies the analysis of mechanism design problems. It states that the researcher, when searching for the best possible mechanism to solve a given problem, can restrict attention to a small subclass of mechanisms, namely those so-called direct mechanisms that satisfy Hurwicz’s condition of incentive compatibility.

While direct mechanisms are not intended as descriptions of real-world institutions, their mathematical structure makes them amenable to analysis. Finding the best of all direct mechanisms for a given problem is often straightforward, and once the best direct mechanism has been found, the researcher can “translate back” that mechanism into a more realistic mechanism. By this seemingly roundabout method, researchers have been able to solve problems of institutional design that would otherwise have been effectively intractable. The first version of the revelation principle was formulated by Gibbard (1973). Several researchers – including Dasgupta, Hammond and Maskin (1979) and Myerson (1979) – independently extended it to the standard notion of Bayesian Nash equilibrium, which has proved particularly fruitful for subsequent research. Myerson (1979, 1982, 1986) developed the principle in its greatest generality and pioneered its application to specific economic problems such as auctions and regulation.

The revelation principle has transformed the analysis of economic mechanisms. One problem remains, however. In many cases, one mechanism admits several different equilibria.³ Even if the best outcome is achieved in one equilibrium, other, inferior equilibria may also exist. For example, conventional double auctions tend to have many equilibria, some of which are associated with very low volumes of trade. Can a mechanism be designed such that allits equilibria are optimal? The first general solution to this problem was given by Eric Maskin (1977). The resulting theory, known as implementation theory, is a key part of modern mechanism design.

A detailed example: bilateral trade

Mechanism design theory offers many powerful results that may seem quite abstract. In order to illustrate the underlying principles in an accessible way, we present a detailed (albeit still incomplete) analysis of a simple example.

Suppose that Erika owns an indivisible object, for instance a piano. She is considering selling the piano to a prospective buyer, we can call him Peter. Erika and Peter each value the piano. Suppose that the piano is worth x to Erika and y to Peter. (That is, Erika would be happy to sell it at any price above x but would prefer to keep it if the price is below x, and conversely for Peter.) They may be able to agree on a price so that both of them gain from the transaction, but only if the piano is of more value to Peter than to Erika (that is, only if y>x). For each of them, the utility gain from a transaction equals the difference between the agreed price and the value each of them ascribes to the piano. If the agreed price is p, then Erika’s utility gain is p-x and Peter’s gain is y-p. The total gain from trade is thus p-x+y-p=y-x. If no trade occurs, then no party obtains any utility gain, so we are looking for a mechanism in which trade will always occur if and only if Peter’s evaluation of the piano is higher than Erika’s.

Now suppose that neither Peter nor Erika knows how the other values the piano, so they each have private information about their own valuation. What kind of mechanism could they use to trade with each other? One possibility is that Erika makes a take-it-or-leave-it offer to Peter. Another possibility is that Peter makes such an offer to Erika. A third possibility would be a so-called double auction, a mechanism in which both parties simultaneously announce a price at which they are willing to trade, and, if Peter’s offer exceeds Erika’s, they trade at the price half way between the two proposed prices (or according to some other pre-specified splitting rule).

However, none of these three mechanisms has the property that trade always occurs if the buyer’s evaluation is higher than that of the seller. For example, if Erika makes a take-it-or-leave-it offer, then it is in her interest to set the price above the actual value she ascribes to the piano. If she sets a price exactly equal to her own valuation, she does not care whether Peter buys or not. If she sets a slightly higher price, she does better – gaining something if Peter buys, and losing nothing if he does not. Peter will of course accept her offer only if the proposed price is equal to or less than the value he ascribes to the piano. So, even if Erika values the piano less than Peter, she may end up proposing a price that is higher than Peter is prepared to pay. The argument is of course analogous if it is instead Peter who makes an offer.

The double auction would realize all gains of trade if traders were to bid according to their private valuation, that is, if Erika announced the bid p=x and Peter the bid p´=y, since then trade would occur if and only if y exceeds x. However, Erika and Peter will not bid according to their valuations, because Erica benefits from bidding above her valuation (in order to obtain a higher price) and Peter benefits from bidding below his valuation (in order to obtain the object at a lower price). To see why, consider Erika’s problem. By bidding slightly above her valuation, Erika knows that she forgoes the opportunity to trade in case her valuation is just about the same as Peter’s bid. But Erika loses virtually nothing from the forgone trade, because (i) the loss in trading probability is small, and (ii) the price is almost the same as Erika’s valuation. On the other hand, whenever Peter’s bid substantially exceeds Erika’s, Erika’s higher bid remains below Peter’s. In these cases, there is still trade, and Erika receives a higher price than if she were to bid truthfully. This (first-order) gain outweighs the (second-order) loss from forgone trade.

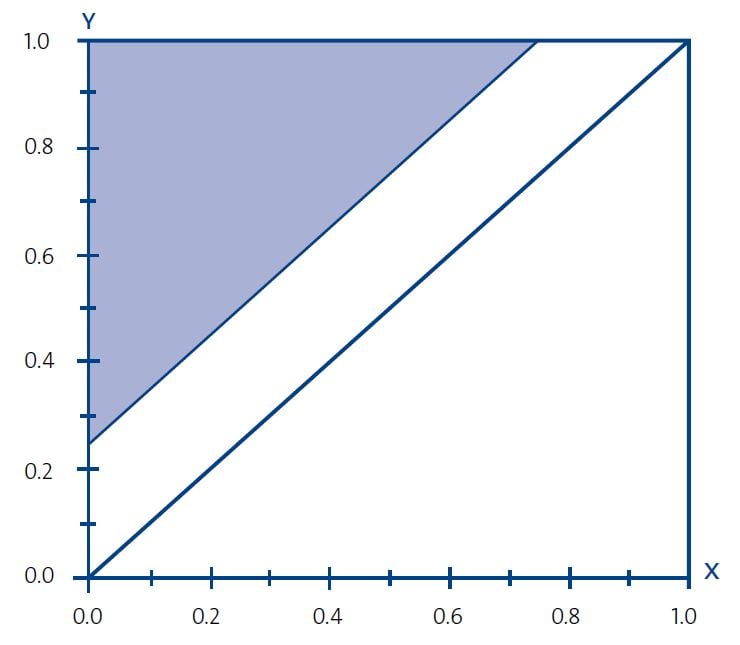
The outcome is illustrated in the diagram, where Erika’s valuation, x, is plotted on the horizontal axis and Peter’s valuation, y, on the vertical axis. Ideally, trade should occur whenever y>x, that is, for all valuation pairs in the large triangle above the diagonal. In equilibrium, however, trade will occur only in a subset of this triangle. For instance, if we think of Erika and Peter as randomly drawn from a population in which the valuations of pianos are uniformly distributed between zero and one, and if Erika and Peter use linear bidding strategies (that is, their bidding prices are linear functions of their valuations), then the best possible equilibrium outcome is that trade occurs in the shaded area – the smaller, upper triangle._⁴ In other words, there is trade if and only if Peter’s valuation y exceeds Erika’s valuation x by a certain positive amount. (In the example, there is trade if and only if Peter’s valuation exceeds Erika’s valuation by 1/4.)

The double auction described above is formally identical with a direct mechanism; namely the mechanism whereby each agent is asked to report his or her valuation of the object at hand to a “center,” and where the object changes hands if and only if the seller’s valuation exceeds that of the buyer, at a price that lies half way (or at any other pre-specified point) between the announced valuations. This direct mechanism would realize all gains of trade, and hence be Pareto efficient⁵, if the agents announced their valuations truthfully. However, for the reasons given above for the double auction, this particular outcome is not incentive compatible: the seller will have an incentive to inflate her valuation and the buyer will have an incentive to deflate his. Truthful reporting of private information is incompatible with equilibrium.

This situation is quite general. Impossibility results established by Laffont and Maskin (1979) and Myerson and Satterthwaite (1983) show that no incentive compatible direct mechanism which satisfies voluntary participation has the property that trade occurs if and only if there are gains from trade, that is, if and only if x<y in our example. By the revelation principle, we can then infer that no mechanism whatsoever can realize all gains from trade. In other words, classical Pareto efficiency is incompatible with voluntary participation and free trade in this example.

The remarkable power of mechanism design theory is that it does not stop here. It allows a characterization of the best mechanism of all conceivable mechanisms. Specifically, Myerson and Satterthwaite (1983) established a precise upper limit for the expected gains from trade that are realizable in any trading mechanism in bilateral situations like this. Moreover, they showed that this upper limit can be realized by way of a double auction. That is, no mechanism can ensure a better outcome than the double auction equilibrium outcome described above.⁶

Concluding remarks

The example shows why markets in general, and auctions in particular, can be efficient institutions for the allocation of private goods. However, efficiency does not imply that an institution will be chosen by those who have the power to select it. Instead, we may expect the choice of institution to reflect the interests of the designer. Fortunately, mechanism design theory can equally well be used to analyze such situations and explain what mechanisms (menus of price offers, bundling of products, auctions etc.) that sellers and buyers prefer, thus providing a theory of which market institutions will emerge. Myerson (1981) and Maskin and Riley (1984) are two leading examples of work in this direction.

Whereas the study of optimal trading institutions is one important application, mechanism design theory has a much broader scope, and it has been used to sharpen the analysis of many other issues in economics and political science. For example, the theory admits a sophisticated analysis of institutions for the provision of public goods, of optimal forms of regulation, and of voting schemes. For a discussion of these and other applications, we refer to our scientific background article (See Links and further reading below).

Notes

1. Goods are called private if one person’s consumption of them precludes their consumption by another person. Typical examples are food and clothes.

2. Goods are called public if one person’s consumption of them does not preclude consumption by others. Typical examples are television programs and (uncongested) roads.

3. Equilibrium is attained when all participants in the mechanism send a message that is in their own best interest. More precisely, an equilibrium is a set of messages, one for each participant, such that each participant sends a message that maximizes his or her own expected payoff, given the other participants’ messages.

4. This result was first proved by Chatterjee and Samuelson (1983).

5. An allocation is called Pareto efficient if there is no other feasible allocation that makes both parties better off.

6. This is not to say that a standard double auction is necessarily the best mechanism for Erika and Peter. The double auction has other less efficient equilibria too. A natural question is therefore whether the same expected surplus can be realized by a mechanism that has a unique equilibrium. Palfrey and Srivastava (1991), building on the work of Maskin (1977), demonstrate that the answer is affirmative.

Links and further reading

More information about this year’s prizes, including a scientific background article, is to be found at the Royal Swedish Academy of Sciences’ website, www.kva.se, and at http://nobelprize.org. You can also see the press conference there as web-TV. Further information about exhibitions and activities concerning the Nobel Prizes is available at www.nobelmuseum.se.

Original scientific articles

Hurwicz. L. (1960): “Optimality and informational efficiency in resource allocation processes”, in Arrow, Karlin and Suppes (eds.), Mathematical Methods in the Social Sciences, Stanford University Press.

Hurwicz L. (1972): “On informationally decentralized systems”, in Radner and McGuire, Decision and Organization, North-Holland.

Maskin E. (1977): “Nash equilibrium and welfare optimality”. Paper presented at the summer workshop of the Econometric Society in Paris, June 1977. Published 1999 in the Review of Economic Studies 66, 23–38.

Myerson R. (1981): “Optimal auction design”, Mathematics of Operations Research 6, 58–73

Introductury scientific articles

Baliga, S. and E. Maskin (2003): “Mechanism design for the environment”, in K. Mäler and J. Vincent (eds.), Handbook of Environmental Economics. Elsevier Science, Amsterdam.

Serrano, R. (2004): “The theory of implementation of social choice rules”, SIAM Review 46, 377–414.

Mas-Colell, A., Whinston M., and J. Green (1995): Microeconomic Theory. Oxford University Press

The Laureates

LEONID HURWICZ
University of Minnesota, MN, USA, Department of Economics
1008 Heller Hall, 271 19th Ave S, Minneapolis, MN 55455 USA
www.econ.umn.edu/faculty/hurwicz

US citizen. Born 1917 in Moscow, Russia. Regents Professor Emeritus of Economics at University of Minnesota, Minneapolis, MN, USA.

ERIC S. MASKIN
Institute for Advanced Study, NJ, USA
Einstein Drive, Princeton, NJ 08540 USA
www.sss.ias.edu/community/maskin.php

US citizen. Born 1950 in New York City, NY, USA. Ph.D. in Applied Mathematics in 1976 at Harvard University, Cambridge, MA, USA. Albert O. Hirschman Professor of Social Science at Institute for Advanced Study, Princeton, NJ, USA, since 2000.

ROGER B. MYERSON
University of Chicago, IL, USA, Department of Economics
1126 East 59th Street, Chicago, IL 60637 USA
http://home.uchicago.edu/~rmyerson

US citizen. Born 1951 in Boston, MA, USA. Ph.D. in Applied Mathematics in 1976 at Harvard University, Cambridge, MA, USA. Glen A. Lloyd Distinguished Service Professor at University of Chicago, IL, USA, since 2007.

© The Royal Swedish Academy of Sciences