Popular information
Information for the public:
What limits the measurable? (pdf)
Populärvetenskaplig information:
Var går gränsen för det mätbara? (pdf)

The Nobel Prize in Physics 2005
This year’s Nobel Prize in Physics is awarded to three scientists in the field of optics. Roy Glauber is awarded half of the Prize for his theoretical description of the behaviour of light particles. John Hall and Theodor Hänsch share the other half of the Prize for their development of laser based precision spectroscopy, that is, the determination of the colour of the light of atoms and molecules with extreme precision.
What limits the measurable?
Waves or particles?
We get most of our knowledge of the world around us through light, which is composed of electromagnetic waves. With the aid of light we can orient ourselves in our daily lives or observe the most distant galaxies of the universe. Optics has become the physicist’s tool for dealing with light phenomena. But what is light and how do various kinds of light differ from each other? How does light emitted by a candle differ from the beam produced by a laser in a CD player? According to Albert Einstein, the speed of light in empty space is constant. Is it possible to use light to measure time with greater precision than with the atomic clocks of today? It is questions like these that have been answered by this year’s Nobel Laureates in Physics.
In the late 19th century it was believed that the electromagnetic phenomena could be explained by means of the theory that the Scottish physicist James Clerk Maxwell had presented; he viewed light as waves. But an unexpected problem arose when one tried to understand the radiation from glowing matter like the sun, for example. The distribution of the strength of the colours did not agree at all with the theories that had been developed based on Maxwell’s original work. There should be much more violet and ultraviolet radiation from the sun than had actually been observed.
This dilemma was solved in 1900 by Max Planck (Nobel Prize, 1918), who discovered a formula that matched the observed spectral distribution perfectly. Planck described the distribution as the result of the inner vibrational state of the heated matter. In one of his famous works a hundred years ago, in 1905, Einstein proposed that radiation energy, i.e. light, also occurs as individual energy packets, so-called quanta. When such an energy packet of this kind enters the surface of a metal, its energy is transferred to an electron, which is released and leaves the material – the photoelectric effect, which was included in Einstein’s Nobel Prize in 1921.
Einstein’s hypothesis means that a single energy packet, later called a photon, gives all its energy to just one electron. Thus we can count the quanta in the radiation by observing and counting the number of electrons, that is, the electric current that comes from the metal surface. Almost all later light detectors are based on this effect.
When the quantum theory was developed in the 1920s, it met with difficulties in the form of senseless, infinite expressions. This problem was not solved until after the Second World War, when quantum electrodynamics, QED, was developed (Nobel Prize in Physics 1965 to Tomonaga, Schwinger and Feynman). QED became the most precise theory in physics and was central to the development of particle physics. However, in the beginning it was judged unnecessary to apply QED to visible light. Instead it was to be treated as an ordinary wave motion with a number of random variations in intensity. A detailed quantum theoretical description was considered unnecessary.
Organised and random light
Until the development of the laser and similar devices, most light phenomena could be understood by Maxwell’s classical theory. An example is shown in fig. 1 a, where the light falling through two slits displays a periodic pattern of intensity on a screen. If the light consists of a single wavelength, is coherent, (see fig. 2 a), its intensity is generally speaking zero in the minimal areas.
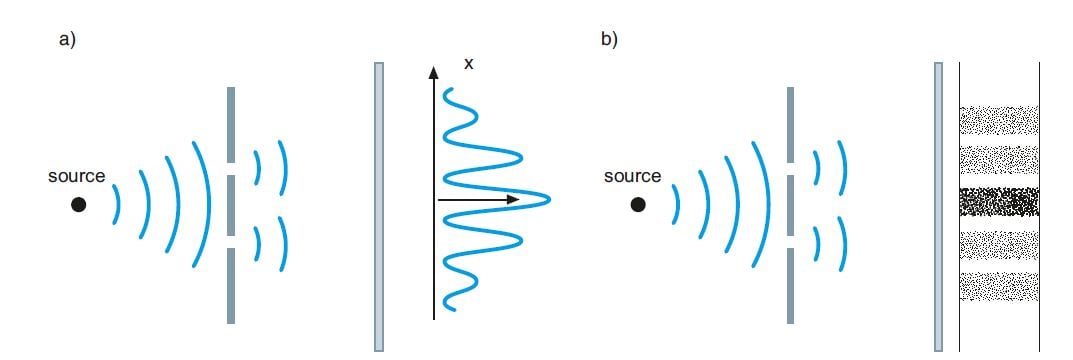
Figure 1. The difference between a classical and a quantum physics observation of light. The passage of light through two slits when it is observed as a) an electromagnetic wave motion and b) a flow of particles. Note that the same interference pattern occurs as the interaction between two waves in the first case or as the distribution of individual particles in the second case.
© The Royal Swedish Academy of Sciences
A more realistic description is required when considering the light from a light bulb. Its light waves have different frequencies and wavelengths and are at the same time out of phase with each other. We see the source as affected by random noise. This incoherent light can be described as in fig. 2 b. Thus, the incoherence makes the interference pattern in fig. 1 a less distinct.
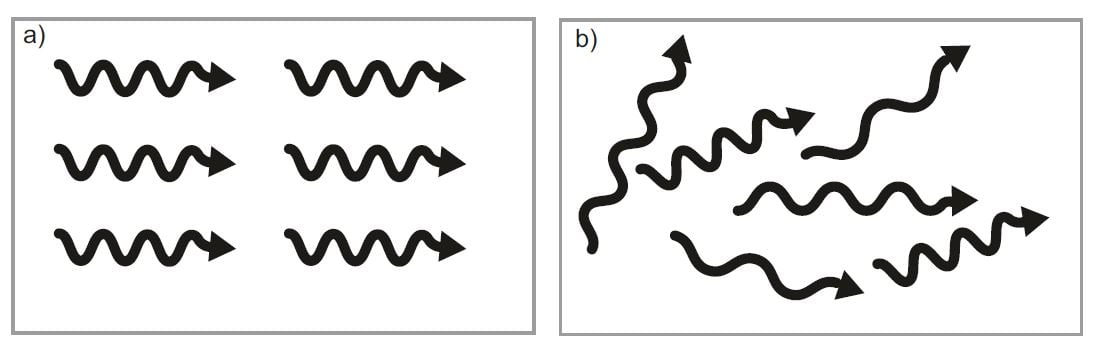
Figure 2. The difference between a) coherent and b) incoherent radiation. In coherent light the rays have the same phase, wavelength and direction.
© The Royal Swedish Academy of Sciences
Previously, most light sources were based on thermal radiation and special arrangements were required in order to observe the interference pattern. This changed when the laser, with its perfectly coherent light, was developed. Radiation with a well-defined phase and frequency was, of course, well known from radio technology. But somehow it seemed strange to see light from a thermal light source as a wave motion – it seemed easier to describe the disorder that stemmed from it as randomly distributed photons.
The birth of Quantum Optics
One half of this year’s Nobel Prize in Physics is awarded to Roy J. Glauber for his pioneering work in applying quantum physics to optical phenomena. In 1963 he reported his results; he had developed a method for using electromagnetic quantization to understand optical observations. He carried out a consistent description of photoelectric detection with the aid of quantum field theory. Now he was able to show that the ”bunching” that R. Hanbury Brown and R. Twiss had discovered was a natural consequence of the random nature of thermal radiation. An ideal coherent laser beam does not display the same effect at all.
But how can a stream of photons, independent particles, give rise to interference patterns? Here we have an example of the dual nature of light. Electromagnetic energy is transmitted in patterns determined by classical optics. Energy distributions of this kind form the landscape into which the photons can be distributed. These are separate individuals, but they have to follow the paths prescribed by optics. This explains the term Quantum Optics. For low light intensities, the state will be described by only a few photons. The individual particle observations will build the patterns of optics after a sufficient number of photoelectrons have been observed. Instead of as in Fig. 1 a, quantum physics would describe the pattern formation as in Fig. 1 b.
An essential feature of the theoretical quantum description of optical observations is that, when a photoelectron is observed, a photon has been absorbed and the state of the photon field has undergone a change. When several detectors are correlated, the system will become sensitive to quantum effects, which will be more evident if only a few photons are present in the field. Experiments involving several photo detectors have been carried out later, and they are all described by Glauber’s theory.
Glauber’s work in 1963 laid the foundations for future developments in the new field of Quantum Optics. It soon became evident that technical developments made it necessary to use the new quantum description of the phenomena.
An observable effect of the quantum nature of light is the opposite of the above-mentioned “bunching” that photons display. This is called “anti-bunching”. The fact is that in some situations photons occur more infrequently in pairs than in a purely random signal. Such photons come from a quantum state that cannot in any way be described as classical waves. This is because a quantum process can result in a state where photons are well separated, in contrast to the results of a purely random process.
Quantum physics sets the ultimate limits and promises new applications
In technical applications, the quantum effects are often very small. The field state is chosen so that it can be assigned well-defined phase and amplitude properties. In laboratory measurements, too, the uncertainty of quantum physics seldom sets the limit. But the uncertainty that nevertheless exists appears as a random variation in the observations. This “quantum noise” sets the ultimate limit for the precision of optical observations. In high-resolution frequency measurements, quantum amplifiers and frequency standards it is in the end only the quantum nature of light that sets a limit for how precise our apparatuses can be.
Our knowledge about quantum states can also be utilised directly. We can get completely new technical applications of quantum phenomena, for example to enable safe encryption of messages within communication technology and information processing.
Laser-based precision spectroscopy
History teaches us that new phenomena and structures are discovered as a result of improved precision in measuring. A splendid example is atomic spectroscopy, which studies the structure of energy levels in atoms. Improved resolution has given us a deeper understanding of both the fine structure of atoms and the properties of the atomic nucleus. The other half of this year’s Nobel Prize in Physics, awarded to John L. Hall and Theodor W. Hänsch, is for research and development within the field of laser-based precision spectroscopy, where the optical frequency comb technique is of special interest. The progress that has been made in this field of science can give us previously unthought of possibilities to investigate constants of nature, find out the difference between matter and antimatter and measure time with unsurpassed precision. Precision spectroscopy was developed when trying to solve some quite clear and straightforward problems as follows below.
How long is a metre?
The problem of determining the exact length of a metre illustrates one of the challenges offered by laser spectroscopy. The General Conference of Weights and Measures, which has had the right to decide on the exact definitions since 1889, abandoned the purely material measuring rod in 1960. This was kept under lock and key in Paris and its length could only with difficulty be distributed throughout the world.
By use of measurements of spectra, an atom-based definition was introduced: a metre was defined as a certain number of wavelengths of a certain spectral line in the inert gas krypton. Some years later also an atom-based definition of a second was introduced: the time for a certain number of oscillations of the resonance frequency of a particular transition in cesium, which could be read off the cesium-based atomic clocks. These definitions made it possible to determine the speed of light as the product of wavelength and frequency.
John Hall was a leading figure in the efforts to measure the speed of light, using lasers with extremely high frequency stability. However, its accuracy was limited by the definition of the metre that was chosen. In 1983, therefore, the speed of light was defined as exactly 299,792,458 m/s, in agreement with the best measurements, but now with zero error! In consequence, a metre was the distance travelled by light in 1/299,792,458 s.
However, measuring optical frequencies in the range round 1015 Hz still proved to be extremely difficult due to the fact that the cesium clock had approximately 105 times slower oscillations. A long chain of highly-stabilised lasers and microwave sources had to be used to overcome this problem. The practical utilisation of the new definition of a metre in the form of precise wavelengths remained problematic; there was an evident need for a simplified method for measuring frequency.
Parallel with these events came the rapid development of the laser as a general spectroscopic instrument. Also, methods for eliminating the Doppler effect were developed, which if not dealt with leads to broader and badly identifiable peaks in a spectrum. In 1981 N. Bloembergen and A.L. Schawlow were awarded the Nobel Prize in Physics for their contribution to the development of laser spectroscopy. This becomes especially interesting when an extreme level of precision can be attained, allowing fundamental questions concerning the nature of reality to be tackled. Hall and Hänsch have been instrumental in this process, through the development of extremely frequency-stable laser systems and advanced measurement techniques that can deepen our knowledge of the properties of matter, space and time.
The frequency comb – a new measuring stick
Measuring frequencies with extremely high precision requires a laser which emits a large number of coherent frequency oscillations. If such oscillations of somewhat different frequency are connected together, the result will be extremely short pulses caused by interference. However, this only takes place if the different oscillations (modes) are locked to each other in what is called mode-locking. (See Fig. 3)
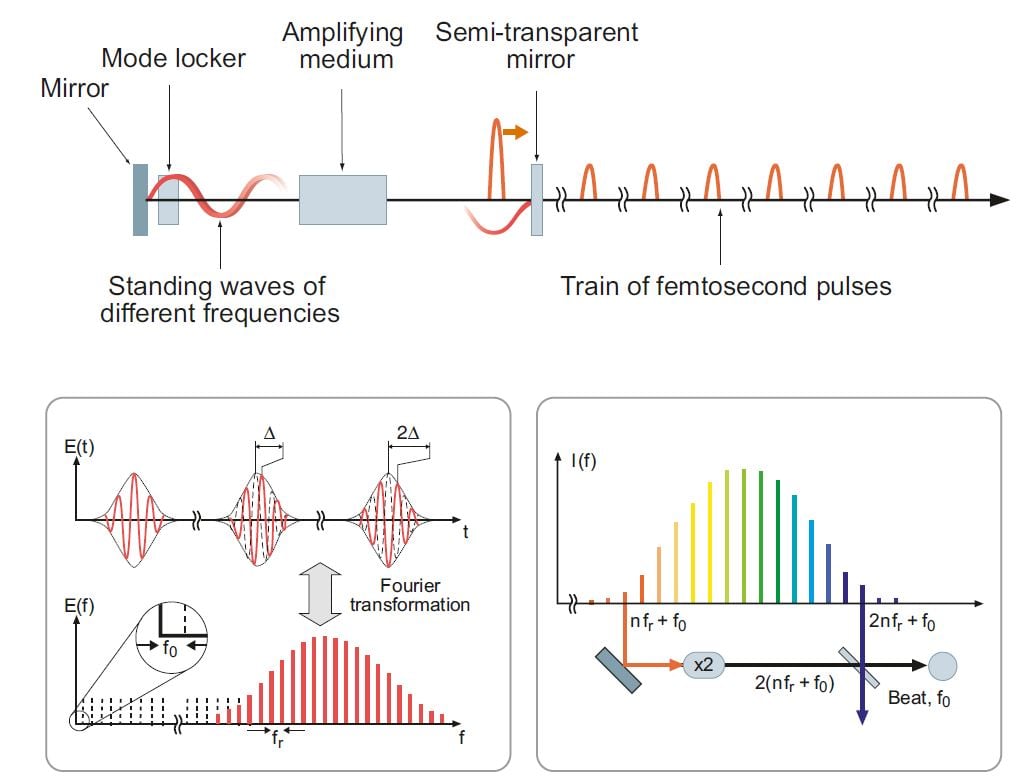
Figure 3. Principles of the frequency comb technique. The upper part of the diagram shows schematically how the laser pulses are created. The lower, left-hand diagram shows both the dependence of the pulses on time, where each pulse contains only a few vibrations, and how the modes are distributed among different frequencies. The spectral distribution consists of a comb of frequencies whose separation is extremely well-defined. The zero point of the spectrum is, however, unknown and represents a displacement fo. By means of non-linear optical techniques the frequencies of the spectrum can be doubled, as shown in the lower, right-hand diagram. Its lowest frequency can then be compared with its original highest frequency and the displacement fo can be determined.
© The Royal Swedish Academy of Sciences
The more different oscillations that can be locked, the shorter the pulses. A 5 fs long pulse (a femtosecond, fs [10-15 s], is a millionth billionth of a second) locks about one million different frequencies, which need to cover a large part of the visible frequency range. Nowadays this can be attained in laser media such as dyes or titanium-doped sapphire crystals. A tiny “ball of light” bouncing between the mirrors in the laser arises because a large number of sharp and evenly distributed frequency modes are shining all the time! A little of the light is released as a train of laser pulses through the partially transparent mirror at one end. Since pulsed lasers also transmit sharp frequencies, they can be used for high-resolution laser spectroscopy. This was realised by Hänsch as early as in the late 1970s and he also succeeded in demonstrating it experimentally. V. P. Chebotayev, Novosibirsk, (d. 1992) also came to a similar conclusion.
However, a real breakthrough did not occur until around 1999, when Hänsch realised that the lasers with extremely short pulses that were available at that time could be used to measure optical frequencies directly with respect to the cesium clock. That is so because such lasers have a frequency comb embracing the whole of the visible range. Thus the optical frequency comb technique, as it came to be called, is based on a range of evenly distributed frequencies, more or less like the teeth of a comb or the marks on a ruler. An unknown frequency that is to be determined, can be related to one of the frequencies along the “measuring stick”. Hänsch and his colleagues convincingly demonstrated that the frequency marks really were evenly distributed with extreme precision. One problem, however, was how to determine the absolute value of the frequency; even if the separation is very well-defined between the teeth of the comb, an unknown common frequency displacement occurs. This deviation must be determined exactly if an unknown frequency is to be measured. Hänsch developed a technique for this purpose in which the frequency also could be stabilised, but the problem was not solved practically and simply until Hall and his collaborators demonstrated a solution around the year 2000. If the frequency comb can be made so broad that the highest frequencies are more than twice as high as the lowest ones (an octave of oscillations), the frequency displacement, f0, can be calculated by simple subtraction involving the frequencies at the ends of the octave (See Fig. 3):
2fn–f2n=2(nfr+f0)–(2nfr+f0)=f0
It is possible to create pulses of this kind with a sufficiently broad frequency range in so-called photonic crystal fibres, in which the material is partially replaced by air filled channels. In these fibres a broad spectrum of frequencies can be generated by the light itself. Hänsch and Hall and their colleagues have subsequently, partly in collaborative work, refined these techniques into a simple instrument that has already gained wide use and is commercially available. An unknown sharp laser frequency can now be measured by observing the beat between this frequency and the nearest tooth in the frequency comb; this beat will be in an easily-managed radio frequency range. This is analogous to the fact that the beat between two tuning forks can be heard at a much lower frequency than the individual tones.
Quite recently frequency comb techniques have been extended to the extreme ultraviolet range, which can be attained by generating overtones from short pulses. This may mean that extreme precision can be achieved at very high frequencies, thereby leading to the possibility of creating even more accurate clocks at X-ray frequencies.
Another aspect of the frequency comb technique is that the control of the optical phase, that it permits, is also of the greatest importance in experiments with ultrashort femtosecond pulses and in ultra-intense laser-matter interaction. The high overtones, evenly distributed in frequency, can be phase-locked to each other, whereby individual attosecond pulses approximately 100 as long (1 as = 10-18 s) can be generated by interference in the same way as in the mode-locking described above. Thus the technique is of the greatest relevance for precision measurements in both frequency and time.
Future prospects
It now seems possible, with the frequency comb technique, to make frequency measurements in the future with a precision approaching one part in 1018. This will soon lead to actualize the introduction of a new, optical standard clock. What phenomena and measuring problems can take advantage of this extreme precision?
The precision will make satellite-based navigation systems (GPS) more exact. Precision will be needed in, for example, navigation on long space journeys and for space-based telescope arrays that are looking for gravitational waves or making precision tests of the theory of relativity. Applications in telecommunication may also emerge.
This improved measurement precision can also be used in the study of the relation of antimatter to ordinary matter. Hydrogen is of special interest. When anti-hydrogen can be experimentally studied like ordinary hydrogen, it will become possible to compare their fundamental spectroscopic properties.
Finally, greater precision in fundamental measurements can be used to test possible changes in the constants of nature over time. Such measurements have already begun to be made, but so far no deviations have been registered. However, improved precision will make it possible to draw increasingly definite conclusions concerning this fundamental issue.
LINKS AND FURTHER READING
At the website of the Nobel Prizes, www.nobelprize.org, one can find more information on this year’s Prizes, e.g. the press conference and an interview with an expert in the field as web-TV. There is also a scientific article, for the more advanced reader.
Literature
Advanced information on the Nobel Prizes in Physics 2005, The Royal Swedish Academy of Sciences
R. Feynman, QED, The Strange Theory of Light and Matter, Princeton Univ. Press, Princeton 1985.
P. L. Knight and L. Allen, Concepts of Quantum Optics, Pergamon Press, Oxford 1983.
H. Paul, Introduction to Quantum Optics, Cambridge Univ. Press, Cambridge 2004.
D. Kleppner, On the matter of the meter, Physics Today, p. 11, March 2001
R. Holzwarth, M. Zimmermann, Th. Udem and T.W. Hänsch, IEEE J. Quant. Electr. 37, 1493, 2001
J.L. Hall, J. Ye, S.A. Diddams, L.-S. Ma, S.T. Cundiff and D.J. Jones, IEEE. J. Quant. Electr. 37, 1482, 2001
Links
www.kva.se/swe/awards/nobel/nobelprizes/press/phyread05.asp
http://nobelprize.org/physics/articles/brink/index.html
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html (look under “Light and Vision”)
http://phys.educ.ksu.edu/
www.aip.org/pt/vol-54/iss-3/p11.html
http://www.physics.mq.edu.au/~drice/quoptics.html
www.aip.org/pt/vol-54/iss-3/p11.html
THE LAUREATES
ROY J. GLAUBER
Physics Department, Harvard University 17 Oxford Street, Lyman 331 Cambridge, MA 02138, USA
www.physics.harvard.edu/people/facpages/glauber.html
US citizen. Born 1925 (80 years) in New York, NY, USA. PhD in physics in 1949 from Harvard
University, Cambridge, MA, USA. Mallinckrodt Professor of Physics at Harvard University.
JOHN L. HALL
JILA, University of Colorado and NIST, Boulder, 440 UCS CO 80309-0440 USA
http://jilawww.colorado.edu/www/faculty/#hall
US citizen. Born 1934 (71 years) in Denver, CO, USA. PhD in physics in 1961 from Carnegie Institute of Technology,
Pittsburgh, PA, USA. Senior Scientist at the National Institute of Standards and Technology and Fellow, JILA, University of Colorado, Boulder, CO, USA.
THEODOR W. HÄNSCH
Ludwig-Maximilians-Universität, Schellingstr. 4, 80799 Munich Germany
www.mpq.mpg.de/~haensch/htm/Haensch.htm
German citizen. Born 1941 (63 years) in Heidelberg, Germany. PhD in physics in 1969 from University of Heidelberg.
Director, Max-Planck-Institut für Quantenoptik, Garching and Professor of Physics at the Ludwig-Maximilians-
Universität, Munich, Germany.
© The Royal Swedish Academy of Sciences
Nobel Prizes and laureates
Six prizes were awarded for achievements that have conferred the greatest benefit to humankind. The 12 laureates' work and discoveries range from proteins' structures and machine learning to fighting for a world free of nuclear weapons.
See them all presented here.
